插头 DP,指的是基于连通性的状态压缩 DP。本文是对陈丹琦的论文尝试进行理解的学习记录,不可避免地会出现错误之处、以及对原文的直接引用。也请读者见谅。
本文在写作过程中,大量参考了idyllic 大佬的插头 DP 博客,并借用了里面的部分图片和插头 DP 的解释。他的博客对我的帮助很大,在此特别感谢。
从旅行商问题开始
在有权无向图中,求从起点到某个终点,必须经过所有点,且每个点只经过一次的问题,被称为 Hamilton (旅行商)问题。
以 P1433 吃奶酪为例。
题目简介:房间里放着 $n$ 块奶酪。一只小老鼠要把它们都吃掉,问至少要跑多少距离?老鼠一开始在 $(0,0)$ 点处。
如果考虑暴力解法,我们就需要列出所有 $n$ 个点的全排列,共有 $n!$ 个,一种全排列就是一种可能的路径。对每个全排列,我们用简单的加法计算出其路径的长度,共有 $n$ 次。最后找到所有路径中的最短路径,时间复杂度为 $O(n \times n!)$,显然不太好。
重新考虑,利用一点贪心的思路,我们先考虑一个较小的范围,在其中找到最好的路径;然后将范围逐步扩大,从局部最优解逐步推向全局最优解。这是一个不错的 DP 思路。
关于本题如何进行状压 DP,本文不再赘述。其时间复杂度为 $O(n^2 \times 2^n)$,显然比暴力解法更好。状压 DP 主要应用于 **集合问题** 中。当 DP 问题是集合时,把这个集合的 **组合或排列** 用一个 **二进制数** 表示,这个二进制数的 $0$ 和 $1$ 的组合就可以用来表述 **集合的一个子集**,从而把 DP 状态的转移转化为二进制的位操作。
在陈丹琦的论文中对其特点给出了非常精准的概括:
- 数据规模的某一维或某几维非常小。
- 具有动态规划的两个基本性质:最优性原理和无后效性。
升级的旅行商:互相关联的决策
在旅行商问题中,我们的每次选择是独立的。从例题中,就是我单独记录每一次每块奶酪要不要吃,不会影响其他奶酪的选择;更抽象地来说,就是我记录的是每个独立元素(即奶酪)的决策;在实际编程中,就是我们枚举每个小集合的每一种情况再选最优解。
但是有些时候,元素之间的决策是互相关联的。在论文中提到这样一种问题:
给出一个 $m \times n$ 的矩阵($m,n \leq 9$),每个格子有一个价值 $V_{i,j}$,要求找一个连通块使得该连通块内所有格子的价值总和最大。
这时候,如果我们再按往常的方式进行每一行的情况枚举,就会发现状况变复杂了:我们每考虑一行,就要重新考虑多行前的状态是否能形成连通块,而且每一次的选择也不能保证局部最优,也就没办法再使用普通的状压 DP。
为了记录这个复杂的情况,我们必然要增加一维,用来记录格子间的连通情况。这时候,本文的主题终于出现:基于连通性状态压缩的动态规划。
概念阐述
术语
插头
插头是一个形象的表述:对一个格子而言,它具有连通上下左右四个格子的能力,就像是它可以插入上下左右四个格子中。如果不存在插头,就说明它没有这种能力。
具体来说,格子 $A(i,j)$ 如果与格子 $B(i,j+1)$ 相连,就可以说格子 $A$ 有一个右插头,格子 $B$ 有一个左插头。
这种表述说明了,插头是成对存在的。例如,如果我们认为格子 $A$ 有一个右插头,那么必然有一个左插头和它相连。
轮廓线
轮廓线实际上在逐格递推的过程中会更常被提及。它划分了已被考虑的部分和未被考虑的部分。我们在进行状态压缩的过程,实际上是在转移轮廓线。
概述
怎么判断题目是插头 DP?抽象地说,如果题目是一道状压 DP,并且要求我们记录连通性信息,那么它就可以用插头 DP 进行解决。具象地说,格点图(棋盘)的汉密尔顿计数(旅行商)、棋盘的黑白染色形成连通块的方案、特定图的生成树计数 等,都是经典的插头 DP 题型。
路径模型
多条路径
下面的分析将以 P5074 Eat the Trees 为例,对插头 DP 进行一个简单的引入。请注意,多条路径问题严格上并不属于插头 DP,但它作为“插头”这一概念的引入是很有意义的。
题目描述:给出 $n \times m$ 的方格,有些格子不能铺线,其它格子必须铺,可以形成多个闭合回路。问有多少种铺法?(保证 $2\le n,m\le 12$)
分析
思考 DP 的一般过程,即状态的转移,在已知前面所有状态的情况下,如何推定当前状态有几种不同的情况?在插头 DP 中,更具体地说,就是已知前面的插头的情况。
根据 DP 的一般过程,我们思考三个问题:第一,“前面的所有状态”指的具体是哪些状态?第二,如何推定当前的状态有哪些可能性?第三,如何转移?
值得注意的是,在很多棋盘模型的状压 DP 问题,如 P2704 [NOI2001] 炮兵阵地 中,我们采用的是逐行转移的写法,因为它很好理解。但在插头 DP 中,我们将更多采用逐格转移的方式。在下一章的插头 DP 模板题中,我们也会简要介绍逐行转移的过程。
前面的状态
我们前面提到了轮廓线,它是已确定状态的格子和未确定状态的格子的分界线。
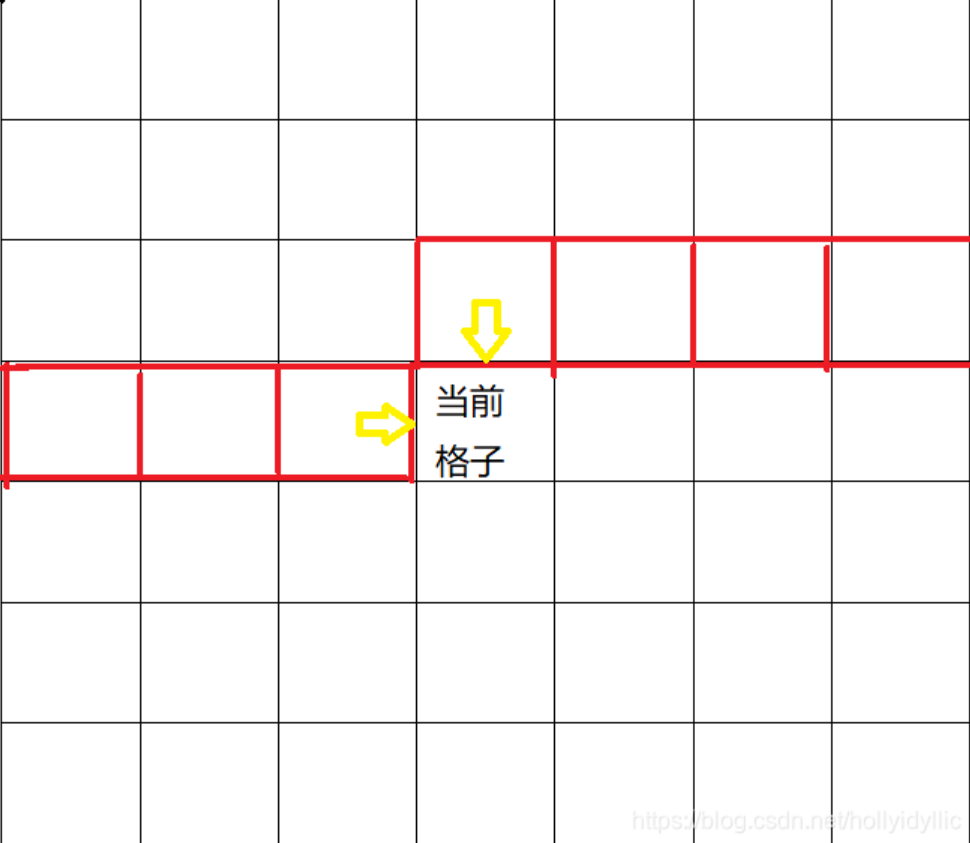
观察这张图,我们发现,我们状态转移的过程只和轮廓线上的插头有关,其他的插头对后续的格子状态没有任何影响。而当前格子的状态只和轮廓线与当前格子的重合部分的插头有关。
当前格子的可能性
为了方便理解,下文中用“左侧插头”表示当前格子左边格子的右插头,“上侧插头”表示当前格子上边格子的 下插头。
我们前面说过,插头是成对存在的。也就是说,左侧插头存在,必有左插头与之对应;上侧插头存在,必有上插头与之对应。否则,插头就没有插在一起,也就没有办法形成路径了。
下面给出了先前的状态和当前格子可能性的关联:
- 有障碍物:没有插头
- 左侧和上侧插头存在:一种,左插头 + 上插头
- 只有左侧插头:两种,左插头 + 右插头/下插头
- 只有上侧插头:两种,上插头 + 右插头/下插头
- 左侧和上侧插头都不存在:一种,右插头 + 下插头
转移过程
显然,枚举完当前这一格的状态后,转移到下一格也只需要用类似的方法。但是有一个特殊的情况:上一行的行末如何转移到下一行的行初?显然,上一行的行末不可能有右插头,下一行的行初不可能有左插头。
程序实现
基础定义
a[13][13] :棋盘大小为 $12 \times 12$dp[13][13][1 << 14]:dp[i][j][state] 表示递推到第 $(i,j)$ 格,且其状态为 $state$ 的情况下的方案总数。其中,状态共有 2^{m+1} 种,因为轮廓线共覆盖了 $m+1$ 条边,每条边上的插头都有存在/不存在两种状态。sta:实际用到的状态数量。
初始化函数 init()
// 初始化
void init()
{
n = read();
m = read();
sta = (1 << (m + 1) - 1);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = read();
memset(dp, 0, sizeof(dp));
}插头 DP 本体
// 插头 DP 本体
void solve()
{
int preI, preJ; // 前一个 (i,j)
dp[0][m][0] = 1; // 初始状态:假设第 0 行(实际并不存在)有一种方案
for (int i = 1; i <= n; i++)
{
// 上一行行末向下一行行初转移
for (int k = 0; k <= sta; k++)
dp[i][0][k << 1] = dp[i - 1][m][k];
for (int j = 1; j <= m; j++)
{
preI = i;
preJ = j - 1;
for (int k = 0; k <= sta; k++)
{
int b1 = (k >> (j - 1)) & 1; // 左侧插头
int b2 = (k >> j) & 1; // 上侧插头
// 情况一:有障碍:不存在插头
if (!a[i][j])
{
if (!b1 && !b2)
dp[i][j][k] += dp[preI][preJ][k]; // 直接转移,继承前一格的状态
}
// 情况五:左侧插头和上侧插头都不存在:下插头+右插头
else if (!b1 && !b2)
dp[i][j][k + (1 << j) + (1 << (j - 1))] += dp[preI][preJ][k];
// 情况三:左侧插头存在,上侧插头不存在:左插头+下插头/右插头
else if (b1 && !b2)
{
dp[i][j][k] += dp[preI][preJ][k];
dp[i][j][k + (1 << (j - 1))] += dp[preI][preJ][k];
}
// 情况四:左侧插头不存在,上侧插头存在:上插头+下插头/右插头
else if (!b1 && b2)
{
dp[i][j][k] += dp[preI][preJ][k];
dp[i][j][k - (1 << (j - 1))] += dp[preI][preJ][k];
}
// 情况二:左侧插头和上侧插头都存在:左插头+上插头
else if (b1 && b2)
{
dp[i][j][k - (1 << j) - (1 << (j - 1))] += dp[preI][preJ][k];
}
}
}
}
printf("%lld\n", dp[n][m][0]);
}下面对状态转移方程进行更进一步的解释:
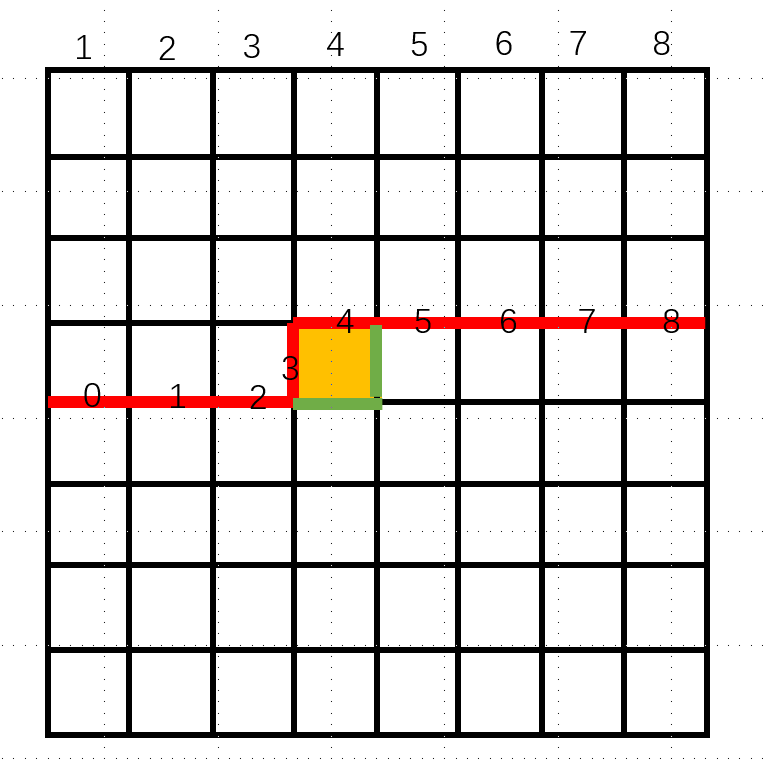
上图展示了一次状态转移。其中轮廓线上的编号代表二进制数存储状态的位置编号,棋盘上的编号代表列数。红线代表上一次状态的轮廓线,绿线代表当前状态的轮廓线。
首先结合图示:当前格子(黄色格子)的左侧插头和上侧插头分别为第三位和第四位,下面将用数对 $(x,y)$ 表示第三、四位的取值,其中 $0$ 为不存在,$1$ 为存在。也就是说,在新状态中,$(i,j)$ 就分别表示下插头和右插头是否存在。
在状态转移方程中具有更一般的表示。假设当前状态为 k,当前列数为 j。那么下插头表示为 1 << (j-1),右插头表示为 1 << j。(结合图示理解)
也就是说,对先前状态 $k = (x,y)$,要让它变成我们已经想好的状态 $k’ = (x’,y’)$,只要相对应地进行计算。例如,如果 $x = 0$,$x’ = 1$,也就是让第一位变成 $1$,只要加上 1 << (j-1) 即可。
下面列出了先前讨论过的所有情况和它们对应的位运算。
- 情况五:上侧插头和左侧插头都不存在,即 $(0,0)$,取下插头和右插头,新状态为 $(1,1)$,表示为
k + (1 << j) + (1 << (j-1)) - 情况三:左侧插头存在,上侧插头不存在,即 $(1,0)$,取左插头 + 下插头/右插头,新状态为 $(1/0,0/1)$,表示为
k或k + (1 << (j-1))。特别注意的是,这边实际上是k - (1 << (j-1)) + (1 << j),最终计算为k + (1 << (j-1)) - 情况四:左侧插头不存在,上侧插头存在,即 $(0,1)$,取上插头 + 下插头/右插头,新状态为 $(0/1,1/0)$,表示为
k或k - (1 << (j-1))。特别注意的是,这边实际上是k + (1 << (j-1)) - (1 << j),最终计算为k - (1 << (j-1)) - 情况二:左侧插头和上侧插头都存在,即 $(1,1)$,取上插头 + 左插头,新状态为 $(0,0)$,表示为
k - (1 << j) - (1 << (j-1))
进一步总结,我们找出一种特殊的情况(如上图),对轮廓线上的插头进行编码,然后根据其二进制的变化进行对应的位运算。
一条路径
下面的分析基于题目 P5056 【模板】插头 DP 完成。
题目描述:给出 $n \times m$ 的方格,有些格子不能铺线,其它格子必须铺,形成一个闭合回路。问有多少种铺法?对于 $100\%$ 的数据,有 $2 \leq n,m \leq 12$。
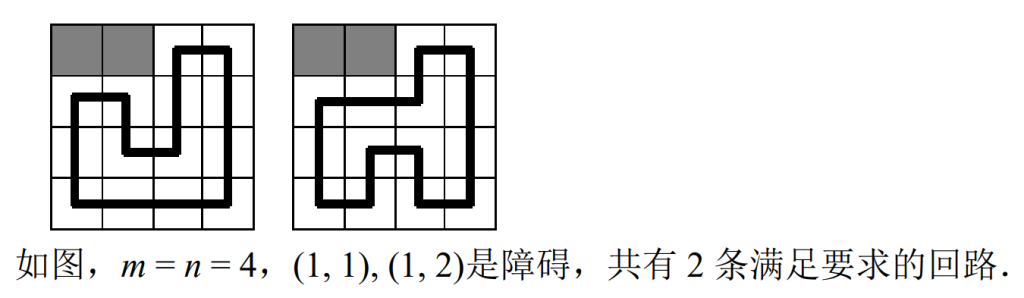
根据上一题,我们只需要再保证一件事情:只有一条回路。
从本题来看,这些线路最终形成了一个 回路,也就是所有可以铺线的格子都 恰好通过两个插头连接 形成了一个 连通块。我们通过这个来判断 转移的状态是否合法。
转移过程
逐行转移
下面先用比较熟悉的逐行转移进行简要的分析。
让我们回到状压 DP 的状态转移。我们像普通的状压 DP 一样考虑每一行每个格子的下插头是否存在。但是如果只是考虑下插头是否存在的话,那么就有可能会出现多个回路的情况:
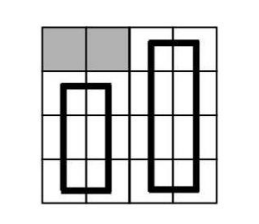
那么我们就要额外记录第 $i$ 行的 $n$ 个格子的连通情况。
逐格转移
现在回到上一题的逐格转移的方式,我们按照从上到下、从左到右的顺序考虑每一格。主要分析的是转移完 $(i,j)$ 这个格子之后哪些信息对后续的决策有影响。
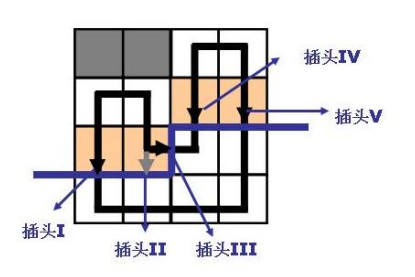
由图可知,与轮廓线直接相连的格子有 $m$ 个($m$ 是列数),直接相连的插头有 $m+1$ 个,其中有 $m$ 个下插头和 $(i,j)$ 的右插头。
与逐行转移类似,我们可以定义 DP 状态: $f(i,j,S_0,S_1)$ 表示第 $(i,j)$ 格,表示这 $m+1$ 个插头是否存在的二进制数 $S_0$,以及这 $m$ 个格子的连通性为 $S_1$ 的方案总数。
如何存储格子之间的连通性
现在的关键点在于,如何用存储格子之间的连通性。

借用上面的图示,运用 并查集 的思想,我们可以把处于联通状态的格子用一个相同的编号编组**,例如第二个过程中,$(1,2)(3,4)$ 具有连通性,我们就可以表示为 ${1,1,2,2}$,然后再转化成二进制进行存储即可。利用这种表示方法,并且使得同一个联通信息具有相同的表示的方法,叫做 *最小表示法*。
有两种最小表示法:
- 所有的障碍格子标记为 $0$,第一个非障碍格子 以及与它相连通的所有格子标记为 $1$,然后继续找第一个非障碍且 未被标记的 以及与它相连通的所有格子标记为 $2$……这是一种更为直观、顺应正常的思路的表示方法。
- 我们考虑将其编码:表示为一个 $m+1$ 位的 $p$ 进制数,$p$ 可以取能达到的最大的连通块的标号加 $1$。
我们考虑将其编码:表示为一个 $m+1$ 位的 $p$ 进制数,$p$ 可以取能达到的最大的连通块的标号加 $1$。
对本题来说,最多出现 $\lfloor \dfrac{n}{2} \rfloor \leq 6$ 个连通块。同时,因为位运算相比于普通运算更快的性,$p$ 最好取 $2$ 的幂。综上,本题的 $p$ 最好取 $8$。
如果需要 大范围修改 联通块的标号,最好将状态 $O(n)$ 解码到一个数组中,修改后再 $O(n)$ 计算出新的 $p$ 进制数。而如果只是需要 局部修改几个标号 的情况下,可以直接用 $(x \div p^{i-1}) \mod p$ 来获取第 $i$ 位的状态,然后 $+k \times p^{i-1}$ 直接对第 $i$ 位进行修改。
进一步优化状态的表示:从最小表示法到括号匹配法
实际上,最小表示法虽然直观、好理解,但是太麻烦了,很多标记在转移过程中是浪费的。让我们重新审视轮廓线。

注意到,为了让整体形成一个回路,必然要一去一回,也就是轮廓线上存在的插头个数一定是偶数个。也就是说,对于一个回路,它有且仅有两个插头,否则它们现在还属于不同的回路。
以上面的图为例,当前的轮廓线,可以看出有四个插头,两条路径;如果将轮廓线向右移动一格,两个插头合并,连通块也就合并,最后只剩下两个插头,一条路径。
这有什么用处呢?让我们首先引入一个性质:
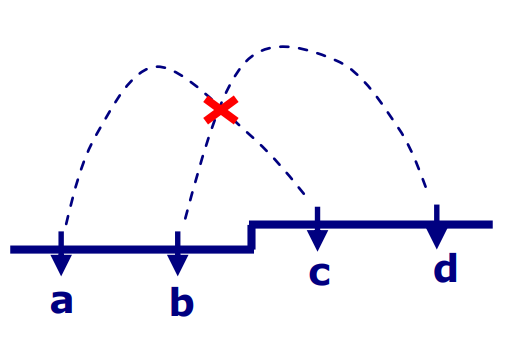
性质:对于轮廓线上从左到右的 $4$ 个插头 $a,b,c,d$,如果 $a,c$ 连通,且与 $b$ 不连通,那么 $b,d$ 一定不连通。
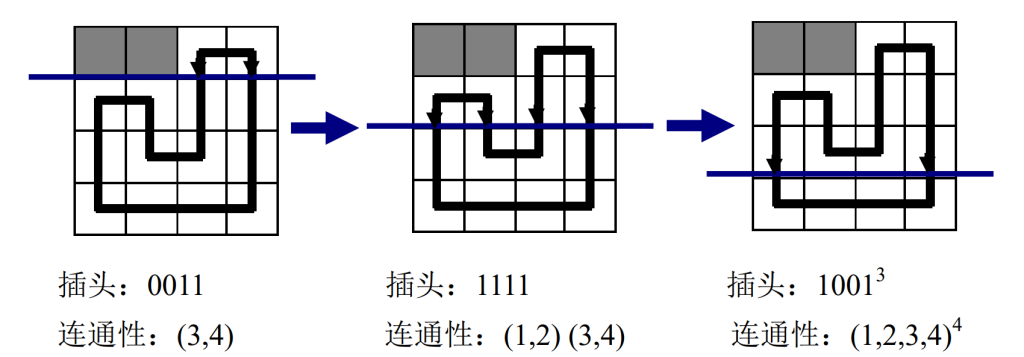
证明(反证法):如果a, c连通,b, d连通,那么轮廓线上方一定至少存在一条a到c的路径和一条b到d的路径.如图,两条路径一定会有交点,不妨设两条路径相交于格子P,那么P既与a, c连通,又与b, d连通,可以推出a, c与b, d连通,矛盾,得证.(引自原论文)
根据这个性质,我们就发现它完美符合括号匹配:两两配对,不会交叉。我们用一个三进制的数表示:$0$ 表示没插头,$1$ 表示左括号,$2$ 表示右括号。
关于括号匹配:用一个简单的例子,在一个复杂的多项式当中,如果有很多括号,我们可以通过类似“栈”的方式将它们两两匹配在一起。
不过,考虑到位运算比普通运算更快,实际应用的时候最好用四进制表示。
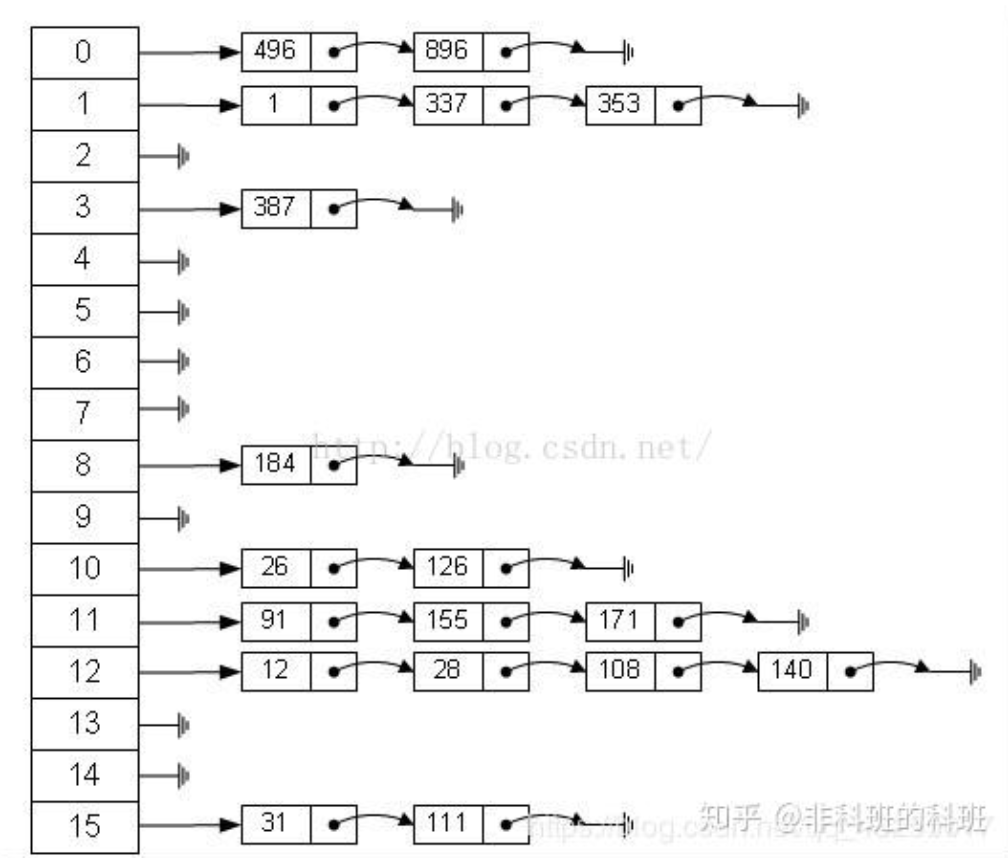
下面验证括号匹配编程实现的可行性:我们知道括号匹配的合法数是一个卡特兰数,它的有用状态并不足以支撑所有状态的最大复杂度。考虑利用哈希映射,这样就可以有效利用可行状态。
状态表示的优化:压缩维度
让我们进一步优化状态的表示。刚才的思路下,我们选择记录两个状态:每行格子是否有下插头,以及格子之间的连通性,以保障最后只有一条回路。
然而,这两个状态之间也是有关联的。如果一个格子没有下插头,那么它就不会和下面的格子连接。它的连通性不会影响下面的格子的选择。所以这个信息的记录是不必要的。
因此,我们将这两个状态合并:如果这个格子没有下插头,直接记为 $0$,否则,记录其连通性。上图的三个状态可以被表示为 $f(1,{0,0,1,1})$,$f(2,{1,1,2,2})$,$f(1,{1,0,0,1})$。
状态转移的过程
逐行转移
从第 $i$ 行转移到第 $i+1$ 行,需要枚举第 $i+1$ 行的每个格子的状态(共 $6$ 种情况)。对于任何一个非障碍格子,其是否具有上插头(根据上一行是否有下插头)和左插头(根据左边那一格是否有右插头)是已知的,所以最多只有两种情况,状态转移数为 $2^m$。
枚举完第 $i+1$ 行每个格子的状态之后,需要计算第 $i+1$ 行 第 $n$ 个格子的连通性的最小表示。可以使用 并查集 或者 BFS/DFS,时间复杂度为 $O(n)$,最后将格子的连通性和插头的存在性进行合并。
值得注意的是转移的过程中,为了避免出现多个连通块,除了最后一行,任何时候一个连通分量内至少有一个格子有下插头。
逐格转移
以下面的图说明转移过程的状态:
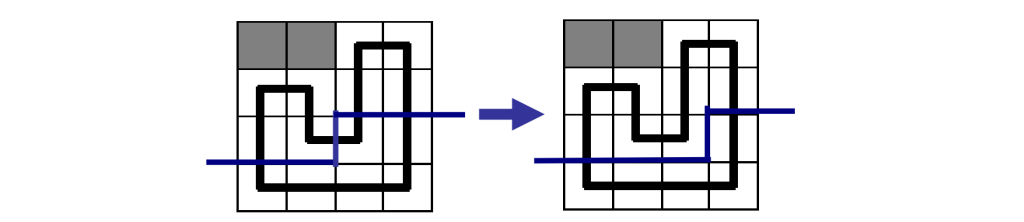
图中演示了从 $f(i,j-1,S)$ 转移到 $f(i,j,S’)$ 的过程。观察轮廓线,发现轮廓线上只有两个插头的状态发生了改变:$(i,j-1)$ 的右插头和 $(i-1,j)$ 的下插头变成了 $(i,j)$ 的右插头和下插头。也就是说,随着轮廓线的转移,只有两个插头会发生变化。
而这两个插头的变化有三种情况。在下面,我们将由好理解的最小表示法推向更高效的括号表示法。
情况一:新建一个连通分量
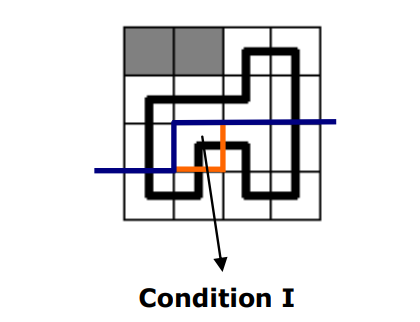
在这里,轮廓线由蓝色变成橙色之后,出现了新的连通分量。这种情况出现于 $(i,j)$ 有右插头和下插头,新建的两个插头相通且不与其他插头联通。这种情况需要将这两个插头连通分量标号标记为一个未标记过的正数,重新扫描保证新的状态满足最小表示。
即 左侧和上方都没有括号,新的连通分量即产生了一个左括号和一个右括号。
情况二:合并两个连通分量
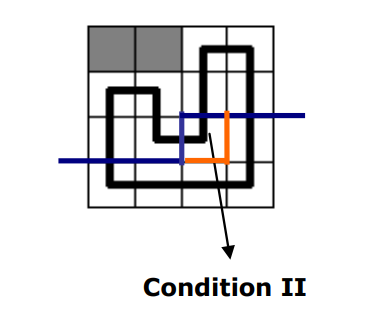
在这里,原本两个不相连的连通分量被合并了。这种情况出现于 $(i,j)$ 有左插头和上插头,且这两个插头本身尚不连通,就将这两个插头所处的连通分量合并,标记相同的连通块标号,再扫描保证最小表示。而如果这两个插头本身是联通的,只会出现在最后一个格子上,这说明出现了一个回路。
即 左侧和上方都有括号,那么连通块合并,这两个括号都要被去掉。共有三种情况:
- 都是左括号:那么后方最近的两个右括号,它们与这两个左括号匹配,为了保证删掉这两个左括号之后依旧括号匹配,就把右方第一个右括号改成左括号。
- 都是右括号:同理的,把左方第一个左括号改成右括号。
- 右括号 + 左括号:直接删掉即可。因为删去后仍旧符合括号匹配。
- 左括号 + 右括号:表示形成回路。不用操作,因为只有可能在最后一个格子上出现。
情况三:保持原来的连通分量
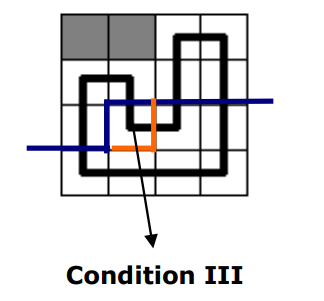
在这里,原本存在两个连通分量,轮廓线转移之后还是两个连通分量。这种情况是 $(i,j)$ 的上插头和左插头恰好有一个,右插头和下插头也恰好有一个。下插头或右插头相当于是上插头或左插头的延续。连通块标号相同,且不会影响其他插头的连通块标号。
这里,即 左括号/右括号 + 没括号 / 没括号 + 左括号/右括号,将当前格子伸出去的插头标记为 左括号/右括号。
回顾
让我们回顾一下上面的内容。
我们定义 DP 状态为 $f(i,j,S)$,指的是转移完第 $(i,j)$ 格,且状态为 $S$ 的方案总数。$S$ 是每格插头是否存在和是否具有连续性的合并,如果这个格子是障碍物或者插头不与轮廓线相连,就记为 $0$,剩下的根据括号表示法编号表示它们是同一个连通分量。$1$ 表示是左括号,$2$ 表示是右括号。
转移过程中会出现七种情况:
- 左侧和上方都没有括号:伸出去的两个插头分别记为左括号和右括号自行匹配
- 左括号/右括号 + 没括号:伸出去的插头记为左括号/右括号
- 没括号 + 左括号/右括号:伸出去的插头记为左括号/右括号
- 左侧和上方都有括号:
- 都是左括号:将右侧第一个右括号改成左括号,再删掉
- 都是右括号:将左侧第一个左括号改成右括号,再删掉
- 右括号 + 左括号:直接删掉
- 右括号 + 左括号:直接删掉
代码实现
#include <iostream>
#include <cctype>
#include <string.h>
#define ll long long
using namespace std;
ll read()
{
ll x = 0, f = 1;
char ch = 0;
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
const ll P = 299987; // 哈希映射的模数
const int maxN = 13 + 10;
const int maxM = 300000 + 10;
const int maxP = (2 << 24) + 10;
ll n, m; // 棋盘的行数和列数
ll ex, ey; // 最后一个非障碍格子的坐标
ll now, last; // 指针
ll ans;
ll a[maxN][maxN]; // 存储地图
ll inc[maxN]; // 存储 2 的幂
ll head[maxM];
ll nxt[maxP];
ll que[2][maxP];
ll val[2][maxP];
ll cnt[2];
void init()
{
n = read();
m = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
char ch = getchar();
while (ch != '*' && ch != '.')
ch = getchar();
if (ch != '.')
a[i][j] = 0;
else
{
a[i][j] = 1;
ex = i;
ey = j;
}
}
inc[0] = 1;
for (int i = 1; i < maxN; i++)
inc[i] = inc[i - 1] << 2;
}
void insert(ll bit, ll num)
{
ll u = bit % P + 1;
for (int i = head[u]; i; i = nxt[i])
if (que[now][i] == bit)
{
val[now][i] += num;
return;
}
nxt[++cnt[now]] = head[u];
head[u] = cnt[now];
que[now][cnt[now]] = bit;
val[now][cnt[now]] = num;
}
void solve()
{
cnt[now] = 1;
val[now][1] = 1;
que[now][1] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= cnt[now]; j++)
que[now][j] <<= 2;
for (int j = 1; j <= m; ++j)
{
memset(head, 0, sizeof(head));
last = now;
now ^= 1;
cnt[now] = 0;
for (int k = 1; k <= cnt[last]; k++)
{
ll bit = que[last][k], num = val[last][k];
ll b1 = (bit >> ((j - 1) * 2)) % 4, b2 = (bit >> (j * 2)) % 4;
if (!a[i][j])
{
if (!b1 && !b2)
insert(bit, num);
}
else if (!b1 && !b2)
{
if (a[i + 1][j] && a[i][j + 1])
insert(bit + inc[j - 1] + inc[j] * 2, num);
}
else if (!b1 && b2)
{
if (a[i][j + 1])
insert(bit, num);
if (a[i + 1][j])
insert(bit - inc[j] * b2 + inc[j - 1] * b2, num);
}
else if (b1 && !b2)
{
if (a[i + 1][j])
insert(bit, num);
if (a[i][j + 1])
insert(bit - inc[j - 1] * b1 + inc[j] * b1, num);
}
else if (b1 == 1 && b2 == 1)
{
int flag = 1;
for (int l = j + 1; l <= m; l++)
{
if ((bit >> (l * 2)) % 4 == 1)
flag++;
if ((bit >> (l * 2)) % 4 == 2)
flag--;
if (!flag)
{
insert(bit - inc[j] - inc[j - 1] - inc[l], num);
break;
}
}
}
else if (b1 == 2 && b2 == 2)
{
int flag = 1;
for (int l = j - 2; l >= 0; l--)
{
if ((bit >> (l * 2)) % 4 == 1)
flag--;
if ((bit >> (l * 2)) % 4 == 2)
flag++;
if (!flag)
{
insert(bit - inc[j] * 2 - inc[j - 1] * 2 + inc[l], num);
break;
}
}
}
else if (b1 == 2 && b2 == 1)
insert(bit - inc[j - 1] * 2 - inc[j], num);
else if (i == ex && j == ey)
ans += num;
}
}
}
}
int main()
{
init();
solve();
printf("%lld", ans);
return 0;
}