顺序表
现在,你是一家魔法工厂里的员工,老板交给你一个棘手的问题——整理好一堆魔力卡片,否则你的工作就会不保。
为了整理好这些卡片,你首先想到了魔法卡册:把这些卡按照某种顺序放在魔法卡册中。你可不想弄得太复杂,所以这是一个只有一行的卡册,它非常长,足够装下所有的卡片。假设一张卡片占据的单位空间是 $1$,一共有 $n$ 张卡片,你最多只需要 $n$ 个单位空间,就可以把这些卡片全部收集整齐。
太好了!你刚才发现了数据结构!大量的扑克牌就是数据,为了更好地管理、收纳、存储、处理这些数据,我们发明了魔法卡册,它就是一种数据结构。
现在让我们进一步研究魔法卡册吧。
这种只有一行的,像一条线一样的魔法卡册是一种最基础的卡册。我们称呼它为线性表。我们按照顺序一张一张把卡片插下去。每一张卡片都是物理上相邻的。——我们叫它顺序表。
不过,魔法卡册并不是普通的卡册,它占据了四次元空间中的一部分,所有放在卡册里的卡片其实都被存储在四次元空间中。所以我们需要先使用魔法开辟出一片空间来制造出这个卡册。首先,你需要先选择一个空间中的点,作为起始点;然后,你需要决定卡册具体有多大,这样四次元空间中一条连续的空间就会被你占据;最后,你还得管理一下卡册里现在存了多少张卡片,万一丢了你可就没工作了。
神秘的四次元空间其实是计算机的内存,内存中每一片区域都有其地址,这就是你选择的起始点的坐标。你使用的魔法——当然就是 C/C++ 语言了!
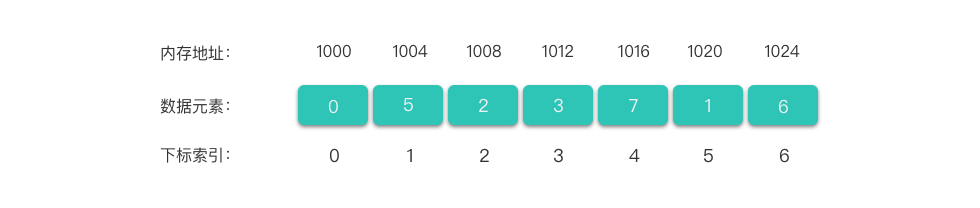
现在让我们开始施法吧。
创造魔法卡册
魔法卡册的构成 | 顺序表的存储结构
在本文中,我们默认你已经掌握了最基础的魔法——C/C++基础语法和某些函数的用法。在下面的代码中,为了方便理解,注释使用文中提到的比喻,读者可以自己将其转化成计算机语言,或对照《数据结构(C语言版 第2版)》(人民邮电出版社,严蔚敏 著)中的代码进行理解。
出于笔者的习惯,文章大部分的代码均为 C++ 风格。
// 顺序表的存储结构
#define MAXSIZE 100 // 卡册的长度
struct SqList // 建立一个结构体,之后可以直接调用这个结构体生成一个顺序表
{
ElemType *elem; // 申请四次元空间,elem 表示首地址
int length; // 卡册现在存储卡片的数量
};
代码中的ElemType表示一种数据类型,它可以是int、double、char或其他用户自定义的数据类型等。此处仅是为了描述统一。
同样都是ElemType的变量也未必是一样的数据类型。请直接将ElemType看作一个空格,在其中填充你需要的数据类型就好。下面解释上面程序中涉及到的一些基础语法,如果你已经忘记了相关的知识可以看看。
#define MAXSIZE 100 // 这是一个宏定义,指的是将 【MAXSIZE】 直接替换成 【100】(不要加分号!) const int MAXSIZE = 100; // 你也可以这样写,这是定义了一个只读(不可改变的)变量。它们有微妙的差别,但在这里都是一样的 struct Sqlist{}; // 定义了一个结构体,并且命名为 Sqlist,之后你可以直接用 Sqlist A 来声明一个类型为 Sqlist 的结构体 A(不要忘了分号!) typedef struct{}Sqlist; // 在 C 语言中要这么写,这样你也可以直接 Sqlist A 了;否则你就要写 struct Sqlist A 了,多麻烦! ElemType *elem; // *代表我们声明的是一个指针。
创造魔法卡册 | 顺序表的创建
在创建的过程中总会发生失败的……失败是成功之母。错误也有很多种,为了方便我们知道究竟发生了什么,我们先来规定一下施展魔法的状态。之后,我们只要通过返回状态,就可以知道我们操作的结果是什么样的。
enum Status
{
OK, // 执行成功
ERROR, // 执行失败
INFEASIBLE, // 参数不合法
OVERFLOW, // 溢出
UNKNOWN // 未知错误
};
enum是一种基本数据类型,用于定义一组常量。默认地,之后的第一个变量就是 $0$,第二个变量就是 $1$ 以此类推。代码enum { Zero, One, Two }就表示
#define Zero 0 #define One 1 #define Two 2这是一种简洁化的表示。
在 C 语言中要这么写:
typedef enum {} Status; // 花括号内内容不变出于笔者的习惯,当某个函数不需要返回值时,且可能出现各种错误类型时,才会使用Status来标识其操作状态。若返回值存在,使用其需求返回值的数据类型;若不会出现错误,则使用void类型。此处的Status只是为了更方便地呈现函数运行中可能发生的错误,展现数据结构本身的原理。在实际的问题解决和情景中,一般不使用Status,请在了解原理后自己根据题目修改,养成自己的代码风格和习惯。接下来我们来创建魔法卡册。分析这个过程:首先,开辟出一片数组空间,其空间大小为
MAXSIZE,且首地址指向这个空间;然后,现在一张卡片都没放,所以length应当是 $0$。
// 创建顺序魔法卡册
Status InitList(SqList &L) // 这个新的空卡册的名字是 L
{
L.elem = new ElemType[MAXSIZE]; // 分配四次元空间
if (!L.elem)
return ERROR; // 分配失败,创建失败
L.length = 0; // 现在一张卡都没放
return OK; // 创建成功
}别忘了函数的格式:【函数类型】+【函数名字】+【传入参数】。
在这里,SqList &L中的&是取地址的意思,代表如果函数中修改了该参数,那么会直接修改其本体,而不是仅在函数域内生效。new用于分配内存。现在我们已经有了卡册,就要往里面装卡片了。在这个过程中,我们假设卡片是通过你来输入的。
// 创建一个线性表,填入 n 个元素
Status CreateList(SqList &L, int n)
{
InitList(L);
for (int i = 1; i <= n; i++)
{
if (L.length + 1 > MAXSIZE)
return ERROR;
cin >> L.elem[i];
L.length++;
}
return OK;
}代码在书写前是加上using namespace std;
的,否则cin就要写成std::cin了。因为这里我们使用了std的命名空间。
这一串输入在 C 语言中要这么写(如果是int类型的话,其他数据类型请自己替换前面的格式符):scanf("%d",&L.elem[i])
接下来,我们只需要把卡片装进去就好了……?等等,你的老板可不单单希望这个卡册只能放卡片,他有各种各样的需求!
使用魔法卡册 | 顺序表的操作
衡量操作时间:时间复杂度
你只是一个打工的牛马,老板的操作有时候很复杂,需要花掉你很多的时间;有时候则比较简单。为了衡量这个过程,你想要知道对于某一个操作,你需要花多长的时间来处理,我们称之为时间复杂度。
关于时间复杂度的定义是复杂艰深的,我们不在此探讨。简单来说,对于 $n$ 张卡片,你的操作次数与 $n$ 越相关,你的时间复杂度越高。这里的相关,指的是随着 $n$ 的增长,你的操作次数的增长情况:例如指数增长、对数增长、平方增长……等等。
举例来说,如果每张卡片都有数字,你的老板想知道两张卡片上的数字:$a$ 和 $b$ 相加的结果 res,显然是
void algorithm() // algorithm 表示算法
{
res = a + b;
}无论有多少张卡片,都和这个结果的计算没有关系,我们说它的时间复杂度是 $O(1)$ 的。
但是如果你的老板想知道这 $n$ 张卡片每一张卡片上的数字相加的结果,就不一样了:
// 假设卡册的名字是 L
void algorithm()
{
int res = 0;
for (int i = 1; i <= n; i++)
res += L[i-1];
return res;
}这个过程中,你的计算过程和 $n$ 是线性增长的,我们说它的时间复杂度是 $O(N)$。
length,但计算时间复杂度、书写公式等时仍说长度为 $n$时间复杂度,只是我们衡量算法优劣的其中一个参考,它不是标准。在现实生活中,硬件、编译器优化、生产环境、数据规模……等等都会影响实际的用时,可能时间复杂度小的用时反而更大……读者在学习的过程中需要谨记这一点,不要过分纠结理论与现实的差别。
我们的思考方式
对待一种操作,我们首先要从老板的想法中抽象出关键。这时候就可以考虑有哪些需要的参数。
然后要思考状态的可能性,并想出什么情况下会触发这些状态例如:
- 错误:什么情况下会导致这个操作不可能实现
- 参数不合法:思考参数的范围等
最后是我们如何实现这种操作,必要的话计算该操作的时间复杂度,衡量最快的算法。
总结地总结我们的思考过程:
- 抽象题意
- 参数范围
- 错误可能
- 算法实现
- 时间复杂度
老板想要知道某个位置上的卡是什么:顺序表的取值/访问
抽象题意:查询顺序表
L的i位置上的值
参数范围:考虑参数 i,因为下标从 $1$ 开始,长度为 length,因此 $1 \leq i \leq n$。
错误可能:无
算法实现:直接利用数组的操作读取
// 查询 L 中第 i 个位置上的元素的值,存储在 ans 中
Status GetElem(SqList &L, int i, ElemType &ans)
{
if (i < 1 || i > L.length) // 判断询问是否合理
return INFEASIBLE; // 询问不合理,即参数不合法
ans = L.elem[i];
return OK;
}时间复杂度:这个过程和 $n$ 无关,其时间复杂度为 $O(1)$。
老板想要修改某个位置上的卡:顺序表的修改
抽象题意:修改顺序表 L 的 i 位置上的值,使其变为 val
参数范围:考虑参数 i,因为下标从 $1$ 开始,长度为 length,因此 $1 \leq i \leq n$。
错误可能:无
算法实现:直接利用数组的操作赋值
// 修改 L 中第 i 个位置的元素,使其变为 val
Status ChangeElem(SqList &L, int i, ElemType val)
{
if (i < 1 || i > L.length)
return INFEASIBLE;
L.elem[i] = val;
return OK;
}时间复杂度:这个过程和 $n$ 无关,其时间复杂度为 $O(1)$。
老板想要找到某张特定的卡:顺序表的查找
抽象题意:查找顺序表 L 第一个值为 val 的元素的位置
参数范围:无
错误可能:可能找不到,这时候可以返回 $0$
算法实现:最简单(但不是最快)的方式是从第一张开始找,一直找到老板说的卡为止。考虑 for 循环
// 查找 L 中第 1 张值为 val 的元素的位置
// 将结果返回,如果找不到,返回 0
int LocateElem(SqList &L, ElemType val)
{
for (int i = 1; i <= L.length; i++)
if (L.elem[i] == val)
return i;
return 0;
}
时间复杂度:分析这个过程,在最糟糕的情况下,我们需要找完这个卡册每一张卡,这个过程与 $n$ 是线性增长的,因此其时间复杂度为 $O(N)$。或者说,因为程序中存在一个 for 循环,这个 for 循环贡献了至多 $n$ 次操作,因此时间复杂度为 $O(N)$。
老板想要在某个位置插入一张卡:顺序表的插入
抽象题意:在顺序表 L 第 i 个位置插入值为 val 的元素
参数范围:$i$ 的取值范围应当为 $1 \leq i \leq n+1$,其中在第 $1$ 个位置和第 $n+1$ 个位置插入分别表示在卡册的最前面和最后面插入。
错误可能:如果现在卡册已经装满了,就绝对无法再插入新的卡片了,说明如果当前长度等于最大上限,就会错误
算法实现:插入分成两个部分:第一,目标位置修改,直接利用数组赋值即可;第二,为了保证数据的完整性,其他元素要后移,这个过程用 for 循环逐步赋值即可。值得注意的是,这个过程应该从后往前进行:比喻地说,如果从前往后,那么前一张卡就盖在第二张卡上面了,我们就不知道第二张卡是什么了。
// 在 L 第 i 个位置插入值为 val 的元素
Status InsertElem(SqList &L, int i, ElemType val)
{
if (i < 1 || i > L.length + 1)
return INFEASIBLE;
if (L.length == MAXSIZE)
return ERROR;
for (int j = L.length; j >= i; j--) // 从最后一张卡到第 i 张卡,全体右移一位
L.elem[j + 1] = L.elem[j];
L.elem[i] = val;
L.length++;
return OK;
}时间复杂度:题目中有一个从 $1$ 到 $n$ 的 for 循环,时间复杂度为 $O(N)$。
老板想要拿出一张卡:顺序表的删除
抽象题意:将顺序表 L 第 i 个位置的元素删除
参数范围:$i$ 的取值范围应当为 $1 \leq i \leq n$
错误可能:无
算法实现:删除分成两个部分:第一,把 i+1 到 length 位置上的元素直接左移,相当于覆盖前一个格子上的卡片;第二,修改 length 的值,使其减一
// 删除 L 第 i 个位置的元素
Status DeleteElem(SqList &L, int i)
{
if (i < 1 || i > L.length)
return INFEASIBLE;
for (int j = i + 1; j <= L.length; j++)
L.elem[j] = L.elem[j + 1];
L.length--;
return OK;
}时间复杂度:同理,题目中有一个从 $1$ 到 $n$ 的 for 循环,时间复杂度为 $O(N)$。
顺序表总结
- 顺序表使用一组连续的内存,来存储一组具有相同类型的数据。
- 访问、改变元素的时间复杂度为 $O(1)$
- 尾部插入、删除元素的时间复杂度为 $O(1)$
- 普通情况插入、删除元素的时间复杂度为 $O(N)$



每一口都是优质好奶ヾ(≧∇≦*)ゝ