【宝宝的第一本数据结构】04 拾遗
|
数据结构
|
622
|
0

11101 字
|
2.8 小时
本文最后更新于161 天前，其中的信息可能已经过时，如有错误请发送邮件到727189340@qq.com

在之前的内容中，我们已经完成了从线性表到链表，再到栈和队列的完整逻辑。然而在这条主干之外，还有一些小小的分支。本文的内容正是为了回顾这些被我们刻意忽略掉（但同样重要）的内容。由于难度的上升和本身知识点的缘故，本节的内容有点干。

在本节拾遗中，我们仍然跳过了课上不会讲的广义表和字符串匹配算法。在未来有时间（或者想看的读者比较多）可能会补充更新。

04 拾遗

重写线性表

首先，让我们重新以类的方式重新写一遍线性表（包括顺式和链式）数据结构。

线性表的顺式存储

顺式存储线性表类声明和实现（sequential_list.h）

#ifndef SEQUENTIAL_LIST_H
#define SEQUENTIAL_LIST_H

#include <iostream>
#include <stdexcept>

// 顺序存储线性表类
template <typename T>
class seqList
{
private:
    T *data;         // 存储元素的数组
    size_t capacity; // 数组的容量
    size_t length;   // 当前元素的个数

    // 扩展数组容量
    void expandCapacity();

public:
    // 构造函数
    seqList(size_t initialCapacity = 10);

    // 析构函数
    ~seqList();

    // 重置表为空表
    void clear();

    // 判断是否为空表
    bool isEmpty() const;

    // 返回表内元素个数
    size_t size() const;

    // 返回某个位置元素的值
    T get(size_t index) const;

    // 返回第一个与某元素位置相同的元素的位置
    int find(const T &element) const;

    // 返回某元素的前驱
    T predecessor(const T &element) const;

    // 返回某元素的后继
    T successor(const T &element) const;

    // 在某个位置前插入某个元素
    void insert(size_t index, const T &element);

    // 删除某个元素
    void remove(const T &element);

    // 遍历表
    void traverse() const;
};

// 构造函数：初始化容量和长度
template <typename T>
seqList<T>::seqList(size_t initialCapacity) : capacity(initialCapacity), length(0)
{
    data = new T[capacity];
}

// 析构函数：释放动态分配的内存
template <typename T>
seqList<T>::~seqList()
{
    delete[] data;
}

// 扩展数组容量，使其变为两倍
template <typename T>
void seqList<T>::expandCapacity()
{
    capacity *= 2;
    T *newData = new T[capacity];
    for (size_t i = 0; i < length; ++i)
        newData[i] = data[i];
    delete[] data;
    data = newData;
}

// 重置表为空表
template <typename T>
void seqList<T>::clear()
{
    length = 0;
}

// 判断是否为空表
template <typename T>
bool seqList<T>::isEmpty() const
{
    return length == 0;
}

// 返回表内元素个数
template <typename T>
size_t seqList<T>::size() const
{
    return length;
}

// 返回某个位置元素的值
template <typename T>
T seqList<T>::get(size_t index) const
{
    if (index >= length)
        throw std::out_of_range("索引超出表的长度");
    return data[index];
}

// 返回第一个与某元素相同的元素的位置
template <typename T>
int seqList<T>::find(const T &element) const
{
    for (size_t i = 0; i < length; ++i)
        if (data[i] == element)
            return i;
    return -1;
}

// 返回某元素的前驱
template <typename T>
T seqList<T>::predecessor(const T &element) const
{
    int index = find(element);
    if (index <= 0)
        throw std::invalid_argument("没有找到该元素的前驱");
    return data[index - 1];
}

// 返回某元素的后继
template <typename T>
T seqList<T>::successor(const T &element) const
{
    int index = find(element);
    if (index == -1 || index >= length - 1)
        throw std::invalid_argument("没有找到该元素的后继");
    return data[index + 1];
}

// 在某个位置前插入某个元素
template <typename T>
void seqList<T>::insert(size_t index, const T &element)
{
    if (index > length)
        throw std::out_of_range("索引超出表的长度");
    if (length == capacity)
        expandCapacity();
    for (size_t i = length; i > index; --i)
        data[i] = data[i - 1];
    data[index] = element;
    length++;
}

// 删除某个元素
template <typename T>
void seqList<T>::remove(const T &element)
{
    int index = find(element);
    if (index == -1)
        throw std::invalid_argument("没有找到该元素");
    for (size_t i = index; i < length - 1; ++i)
        data[i] = data[i + 1];
    length--;
}

// 遍历表
template <typename T>
void seqList<T>::traverse() const
{
    for (size_t i = 0; i < length; ++i)
        std::cout << data[i] << " ";
    std::cout << std::endl;
}

#endif // SEQUENTIAL_LIST_H
为什么不采取类定义和实现分离的方式？
因为我使用了模板函数 template<typename T>，模板函数在 C++ 中是无法分离的，并且合并操作也是被推荐的。对于其他的非模板函数而言，最好还是采取分离的方式。

顺式存储线性表测试（main.cpp）

#include "sequential_list.h"
#include <iostream>

int main()
{
    seqList<int> list;

    // 插入元素
    list.insert(0, 10);
    list.insert(1, 20);
    list.insert(2, 30);
    list.traverse(); // 理论输出：10 20 30

    // 删除元素
    list.remove(20);
    list.traverse(); // 理论输出：10 30

    // 获取元素
    std::cout << "索引为 1 的元素是：" << list.get(1) << std::endl; // 理论输出 10

    // 查找元素
    int pos = list.find(30);
    std::cout << "内容为 30 的元素的位置是：" << pos << std::endl; // 理论输出 1

    // 获取前驱和后继
    std::cout << "元素 30 的前驱是" << list.predecessor(30) << std::endl; // 理论输出 10
    try
    {
        std::cout << "元素 30 的后继是" << list.successor(30) << std::endl;
    }
    catch (const std::invalid_argument &e)
    {
        std::cout << e.what() << std::endl;
    } // 这里的 try 和 catch 是为了捕捉是否抛出异常

    return 0;
}

线性表的链式存储（链表）

在 02 链表 的文章中，我们并没有研究链表的头插法和尾插法，而是粗暴地直接将调用 insert 并不断插入在索引为 0 的位置来创建一个链表。在这里，作为拾遗部分，会给出头插法和尾插法的定义和实现函数，它可以做到将一个数组转化为一个链表。
由于头插法和尾插法的内容比较简单，这里就不再赘述。下面单独给出头插法和尾插法的实现代码。
// 头插法创建链表
template <typename T>
void linkedList<T>::createListHead(const T arr[], size_t size)
{
    clear();
    for (size_t i = size; i-- > 0;)
    {
        node* newNode = new node(arr[i]);
        newNode->next = head;
        head = newNode;
        length++;
    }
}

// 尾插法创建链表
template <typename T>
void linkedList<T>::createListTail(const T arr[], size_t size)
{
    clear();
    node* tail = nullptr;
    for (size_t i = 0; i < size; i++)
    {
        node* newNode = new node(arr[i]);
        if (tail == nullptr)
        {
            head = newNode;
            tail = newNode;
        }
        else
        {
            tail->next = newNode;
            tail = newNode;
        }
        length++;
    }
}

链式存储线性表类声明和实现（linedList.h）

#ifndef LINKED_LIST_H
#define LINKED_LIST_H

#include <iostream>
#include <stdexcept>

template <typename T>
struct Node
{
    T data;
    Node *next;
    Node(const T &data) : data(data), next(nullptr) {}
};

template <typename T>
class linkedList
{
private:
    using node = Node<T>;
    node *head;    // 链表头指针
    size_t length; // 当前元素个数

public:
    // 构造函数
    linkedList();

    // 析构函数
    ~linkedList();

    // 重置表为空表
    void clear();

    // 判断是否为空表
    bool isEmpty() const;

    // 返回表内元素个数
    size_t size() const;

    // 返回某个位置元素的值
    T get(size_t index) const;

    // 返回第一个与某元素相同的元素的位置
    int find(const T &element) const;

    // 返回某元素的前驱
    T predecessor(const T &element) const;

    // 返回某元素的后继
    T successor(const T &element) const;

    // 在某个位置前插入某个元素
    void insert(size_t index, const T &element);

    // 删除某个元素
    void remove(size_t index);

    // 遍历表
    void traverse() const;
};

// 构造函数
template <typename T>
linkedList<T>::linkedList() : head(nullptr), length(0) {}

// 析构函数
template <typename T>
linkedList<T>::~linkedList()
{
    clear();
}

// 重置表为空表
template <typename T>
void linkedList<T>::clear()
{
    node *current = head;
    while (current)
    {
        node *next = current->next;
        delete current;
        current = next;
    }
    head = nullptr;
    length = 0;
}

// 判断是否为空表
template <typename T>
bool linkedList<T>::isEmpty() const
{
    return length == 0;
}

// 返回表内元素个数
template <typename T>
size_t linkedList<T>::size() const
{
    return length;
}

// 返回某个位置元素的值
template <typename T>
T linkedList<T>::get(size_t index) const
{
    if (index >= length)
        throw std::out_of_range("索引超过表长");
    node *cur = head;
    for (size_t i = 0; i < index; i++)
        cur = cur->next;
    return cur->data;
}

// 返回第一个与某元素相同的元素的位置
template <typename T>
int linkedList<T>::find(const T &element) const
{
    node *cur = head;
    size_t index = 0;
    while (cur)
    {
        if (cur->data == element)
            return index;
        cur = cur->next;
        index++;
    }
    return -1;
}

// 返回某元素的前驱
template <typename T>
T linkedList<T>::predecessor(const T &element) const
{
    if (head == nullptr || head->data == element)
        throw std::invalid_argument("无法找到前驱");
    node *cur = head;
    while (cur->next && cur->next->data != element)
        cur = cur->next;
    if (cur->next == nullptr)
        throw std::invalid_argument("无法找到前驱");
    return cur->data;
}

// 返回某元素的后继
template <typename T>
T linkedList<T>::successor(const T &element) const
{
    node *cur = head;
    while (cur && cur->data != element)
        cur = cur->next;
    if (cur == nullptr || cur->next == nullptr)
        throw std::invalid_argument("无法找到后继");
    return cur->next->data;
}

// 在某个位置前插入某个元素
template <typename T>
void linkedList<T>::insert(size_t index, const T &element)
{
    if (index > length)
        throw std::out_of_range("索引不合法");
    node *newNode = new node(element);
    if (index == 0)
    {
        newNode->next = head;
        head = newNode;
    }
    else
    {
        node *cur = head;
        for (size_t i = 0; i < index - 1; i++)
            cur = cur->next;
        newNode->next = cur->next;
        cur->next = newNode;
    }
    length++;
}

// 删除某个元素
template <typename T>
void linkedList<T>::remove(size_t index)
{
    if (index > length)
        throw std::out_of_range("索引不合法");
    if (index == 0)
    {
        node *tmp = head;
        head = head->next;
        delete tmp;
    }
    else
    {
        node *cur = head;
        for (size_t i = 0; i < index - 1; i++)
            cur = cur->next;
        node *tmp = cur->next;
        cur->next = tmp->next;
        delete tmp;
    }
    length--;
}

// 遍历表
template <typename T>
void linkedList<T>::traverse() const
{
    node *cur = head;
    while (cur)
    {
        std::cout << cur->data << " ";
        cur = cur->next;
    }
    std::cout << std::endl;
}

#endif // LINKED_LIST_H

链式存储线性表类测试（main.cpp）

#include "linkedList.h"
#include <iostream>

int main()
{
    linkedList<int> list;

    // 插入元素
    list.insert(0, 10);
    list.insert(1, 20);
    list.insert(2, 30);
    list.traverse(); // 输出：10 20 30

    // 删除元素
    list.remove(1);
    list.traverse(); // 输出：10 30

    // 获取元素
    std::cout << "索引为 1 的元素是：" << list.get(1) << std::endl;

    // 查找元素
    int pos = list.find(30);
    std::cout << "值为 30 的元素位置是：" << pos << std::endl;

    // 获取前驱和后继
    std::cout << "30 的前驱是" << list.predecessor(30) << std::endl; // 输出：10
    try
    {
        std::cout << "30 的后继是：" << list.successor(30) << std::endl;
    }
    catch (const std::exception &e)
    {
        std::cout << e.what() << std::endl; // 输出：无法找到后继
    }

    // 清空列表
    list.clear();
    std::cout << "表是否为空：" << list.isEmpty() << std::endl; // 输出：1（true）

    return 0;
}

双向链表

为了节省篇幅，之后我们仅展示类声明和实现文件。
#ifndef LIST_H
#define LIST_H

#include <iostream>
#include <stdexcept>

template <typename T>
struct Node
{
    T data;                                                             // 节点存储的数据
    Node *prev;                                                         // 指向前一个节点的指针
    Node *next;                                                         // 指向后一个节点的指针
    Node(const T &value) : data(value), prev(nullptr), next(nullptr) {} // 节点构造函数
};

template <typename T>
class List
{
private:
    using node = Node<T>;
    node *head; // 头节点
    node *tail; // 尾节点
    size_t length;

public:
    // 构造函数
    List();

    // 析构函数
    ~List();

    // 在尾部添加元素
    void push_back(const T &value);

    // 在头部添加元素
    void push_front(const T &value);

    // 移除链表尾部的节点
    void pop_back();

    // 移除链表头部的节点
    void pop_front();

    // 检查链表是否为空
    bool empty() const;

    // 返回链表中元素的数量
    size_t size() const;

    // 清空链表
    void clear();
};

// 构造函数
template <typename T>
List<T>::List() : head(nullptr), tail(nullptr), length(0) {}

// 析构函数
template <typename T>
List<T>::~List()
{
    clear();
}

// 在尾部添加元素
template <typename T>
void List<T>::push_back(const T &value)
{
    node *newNode = new Node(value); // 创建新节点
    if (tail)                        // 如果链表不为空
    {
        tail->next = newNode; // 将链表的尾部连接到新的节点
        newNode->prev = tail; // 修改新节点的前驱
    }
    else                // 如果链表为空
        head = newNode; // 直接将该节点作为头节点
    tail = newNode;     // 更新尾部节点
    ++length;           // 增加长度
}

// 在头部添加元素
template <typename T>
void List<T>::push_front(const T &value)
{
    node *newNode = new Node(value);
    if (head)
    {
        head->prev = newNode;
        newNode->next = head;
    }
    else
        tail = newNode;
    head = newNode;
    ++length;
}

// 移除链表尾部的节点
template <typename T>
void List<T>::pop_back()
{
    if (empty())
        throw std::underflow_error("链表为空");
    node *tmp = tail;  // 暂存尾部节点预备删除
    tail = tail->prev; // 更新尾节点
    if (tail)
        tail->next = nullptr;
    else
        head = nullptr;
    delete tmp;
    --length;
}

// 移除链表头部的节点
template <typename T>
void List<T>::pop_front()
{
    if (empty())
        throw std::underflow_error("链表为空");
    node *tmp = head;
    head = head->next;
    if (head)
        head->prev = nullptr;
    else
        tail = nullptr;
    delete tmp;
    --length;
}

// 检查链表是否为空
template <typename T>
bool List<T>::empty() const
{
    return length == 0;
}

// 返回链表中元素的数量
template <typename T>
size_t List<T>::size() const
{
    return length;
}

// 清空链表
template <typename T>
void List<T>::clear()
{
    while (!empty())
        pop_front();
}

线性表知识点拾遗

随机访问

我们之前说过：

这种只有一行的，像一条线一样的魔法卡册是一种最基础的卡册。我们称呼它为线性表。我们按照顺序一张一张把卡片插下去。每一张卡片都是物理上相邻的。—— 我们叫它顺序表。

不过，魔法卡册并不是普通的卡册，它占据了四次元空间中的一部分，所有放在卡册里的卡片其实都被存储在四次元空间中。所以我们需要先使用魔法开辟出一片空间来制造出这个卡册。首先，你需要先选择一个空间中的点，作为起始点；然后，你需要决定卡册具体有多大，这样四次元空间中一条连续的空间就会被你占据；最后，你还得管理一下卡册里现在存了多少张卡片，万一丢了你可就没工作了。

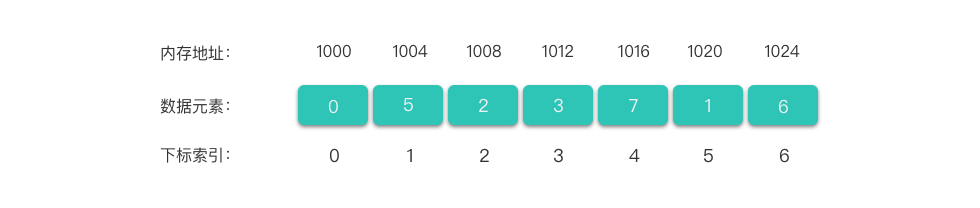
神秘的四次元空间其实是计算机的内存，内存中每一片区域都有其地址，这就是你选择的起始点的坐标。

魔法卡册（我们现在知道它叫线性表了）是四次元空间（即内存）中连续的一段空间，而你选择的起始点，即第一个元素开始的地址，被称为首地址。因为每个元素占据的空间是固定可知的，又因为它只有一条直线，那么无论我们询问第几个元素，我们都可以知道其地址。正如询问小明一秒能跑 5 米，只要小明跑的是直线，又知道小明的起始坐标和它跑的时间，就可以利用公式计算出小明的坐标一样。我们可以用：

$$
下标 i 对应的数据元素地址 = 数据首地址 + i \times 单个数据元素所占内存大小
$$

来计算某个下标的数据元素所在的位置。也就是说，顺序表可以根据下标，直接定位到某一个元素存放的位置。这个能力被称之为随机访问。意思是数据的位置与访问时间无关。链表就不能做到随机访问，我们要找到第 i 个元素的位置，就只能从头节点往下推算。

为什么被称为“随机”呢？这个随机其实可以理解为“随意”。你无需遍历表就可以“随意地”找到某个位置你需要的元素。

线性/有序集合的合并

线性/有序集合的合并是线性表的一种应用。读者可以在学习完之后举一反三其其他的应用。

线性表的合并

线性表的合并是这样一类问题：给定两个集合 $A$ 和 $B$，求其并集。显然，我们只要遍历其中一个集合（例如 $A$），在过程中每遍历到一个元素，就遍历一遍另一个集合（例如 $B$），如果在 $B$ 中找得到这个元素，就跳过；反之，就把这个元素放在 $B$ 集合中。以此类推。

根据这个描述，我们可以写出代码，以顺式存储为例：

#include "sequentialList.h"
#include <iostream>

int tmp; // 临时变量

sequentialList<int> A, B; // 建立两个顺序表

int main()
{
    // 输入两个集合
    std::cout << "请输入 A 集合（回车结束）：";
    while (std::cin >> tmp)
    {
        A.insert(A.size(), tmp);
        if (std::cin.get() == '\n')
            break;
    }
    std::cout << "请输入 B 集合（回车结束）：";
    while (std::cin >> tmp)
    {
        B.insert(B.size(), tmp);
        if (std::cin.get() == '\n')
            break;
    }

    // 合并
    int n = A.size(); // 表 A 的长度

    for (int i = 0; i < n; i++)
    {
        tmp = A.get(i);
        if (B.find(tmp) == -1) // 在 B 中找当前元素没找到
            B.insert(B.size(), tmp);
    }

    std::cout << "合并的结果：" << B.traverse(); // 结果展示
}

显然，解决问题的过程是

for (int i = 0; i < n; i++)
{
    tmp = A.get(i);
    if (B.find(tmp) == -1) // 在 B 中找当前元素没找到
        B.insert(B.size(), tmp);
}

它是一个（隐藏的）三层嵌套 for 循环，get() 的时间复杂度为 $O(1)$，find() 的时间复杂度为 $O(N)$，insert() 若是插入在表末，其时间复杂度为 O(1) 。加上外层的循环，其时间复杂度应为 $O(n \times m)$，其中 $n,m$ 分别是表 $A,B$ 的长度。

在链式存储中， 代码是完全一致的。然而 get() 的时间复杂度为 $O(N)$，find() 的时间复杂度为 $O(N)$，insert() 的时间复杂度为 O(1)。因为 get() 和 find() 都是同一个 for 循环内部嵌套的函数，加上外层的循环，其时间复杂度也为 O(n \times m)，其中 $n,m$ 分别是表 $A,B$ 的长度。

所有函数时间复杂度的分析请回到定义/实现文件中查看。

还能更快吗？
实际上，对于两个集合的合并问题，利用线性表并不是最佳的求解方式。——总有人不满意于此，所以开发出了更多特化解决某些问题的对策性数据结构，我们以后或许会学到。

有序表的合并

在线性表的合并中，我们可能会遇到一种特殊的情况：有序。如果两个集合内的元素都是有序的（例如从小到大），我们又要求合并后的集合仍然保证这种有序性，我们就称之为有序表的合并。

我们可以沿用刚才的做法吗？由于两张表都是有序的，我们固定 $B$（相当于最后合并后的集合是 $B$），遍历到第 $i$ 个元素时，就把集合 $A$ 中值在第 $i$ 个元素的值到第 $i+1$ 个元素的值之间的所有元素插入到第 $i+1$ 个元素前。或许可以这样写：

// 合并
int n = A.size();
int m = B.size();
// 特殊处理比 B 中第一个元素小的元素
for (int i = 0; i < n; i++)
{
    if (A.get(i) < B.get(0))
        B.insert(0, A.get(i));
}
for (int i = 1; i < m; i++)
{
    int left = B.get(i - 1); // 左端点
    int right = B.get(i);    // 右端点
    for (int j = 0; j < n; j++)
        if (A.get(j) > left && A.get(j) < right)
            B.insert(i, A.get(j));
}
std::cout << "合并结果：";
B.traverse();

输出结果：

请输入 A 集合（回车结束）：3 5 8 11
请输入 B 集合（回车结束）：2 6 8 9 11 15 20
合并结果：2 5 3 5 6 8 9 11 15 20

太糟糕了！结果并不是我们想要的！我们重新审视这段代码：虽然想法很美好，但是当我们在 $B$ 中插入 $A$ 中的元素时，$B$ 集合中原本的元素下标可能就改变了，这就导致我们调用函数时本来以为的位置发生了偏移。能不能避免这种情况？我们干脆不要在 $B$ 上直接添加元素，而是新建一个用来输出答案的表（比如说 $C$），这样就不会发生下标的偏移了。还是按照刚才的思路，我们以 $B$ 作为基准，先把 B.get(i) 放进答案集合，然后把 B.get(i) 到 B.get(i+1) 之间的 $A$ 集合中的元素放进答案集合……按照这样的循环，直到结束。

// 合并
int n = A.size();
int m = B.size();
sequentialList<int> C; // 存储最后的答案
// 特殊处理比 B 中第一个元素小的元素
for (int i = 0; i < n; i++)
{
    if (A.get(i) < B.get(0))
        C.insert(C.size(), A.get(i));
}
for (int i = 1; i < m; i++)
{
    C.insert(C.size(), B.get(i - 1));
    int left = B.get(i - 1); // 左端点
    int right = B.get(i);    // 右端点
    for (int j = 0; j < n; j++)
        if (A.get(j) > left && A.get(j) < right)
            C.insert(C.size(), A.get(j));
}
std::cout << "合并结果：";
C.traverse();

该算法的时间复杂度约为 $O(m \times n)$，存在一层外层 for 循环和一层内部 for 循环。值得注意的是，因为我们每次插入 $C$ 都是插入到末尾，其时间复杂度为 $O(1)$。

还能不能再快些！既然表是有序的，那么小于 B.get(1) 的元素一定小于 B.get(2)，但是我们的算法中，还是 for 循环到了这个元素。这就带来了很大的无意义时间开销。现在我们隆重为您介绍一种基础算法、或者说基础思想——

“指针”。

别误会，这里说的“指针”并不是 C 语言意义上的 int *p 的那种指针，其实指的是一个类似于“游标”一样的索引。我们重新思考这个过程，所谓的“合并”，其实也就是“创建了一个新的集合，而其元素全部来自于 $A $和 $B$”而已。那么，我们最终要取得的是一个“递增的集合”，即“每次置入集合的一定是 $A$ 和 $B$ 还没被选中的元素中最小的元素”。而又知道，$A$ 和 $B$ 集合本身就是一个递增的集合，其最左端的元素一定是这个集合中最小的元素。也就是说只要比较这两个集合最左端的元素，我们就等同于找出了“两个集合中最小的元素”。

我们分别用一个指针指向这两个线性表最左端的元素，假设此时 $A$ 集合被指向的元素大于 $B$ 集合被指向的元素，就说 $B$ 是更小的，把它放入数组，指针右移一位，代表“指针左边的都已经被选过了，我们不考虑它们”。继续重复这个过程，直到指针移动出界。

  • 特别地，如果两个元素相等，我们就让 $A$ 集合中的元素进入。
  • 特别地，如果其中一个指针已经“出界”，就说明另一个指针对应的表剩下的元素全部都大于这个指针的表对应的元素，全部加入 $C$ 集合即可。

可以参考下面的图理解这个过程：

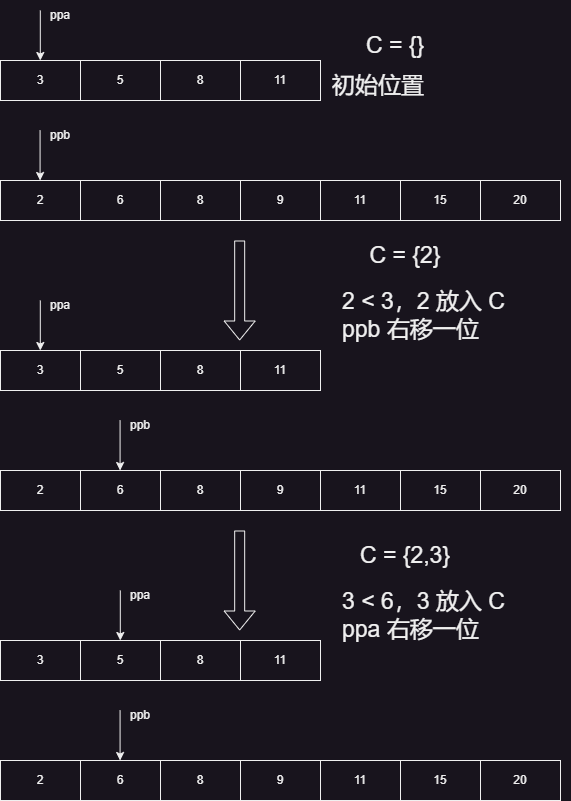
这个 ppa 和 ppb 就叫做指针。

下面展示代码：

// 合并
int n = A.size();
int m = B.size();
sequentialList<int> C; // 存储最后的答案

int ppa = 0, ppb = 0;      // 指针
while (ppa < n && ppb < m) // 直到指针出界
{
    if (A.get(ppa) <= B.get(ppb))
    {
        C.insert(C.size(), A.get(ppa));
        if (A.get(ppa) == B.get(ppb)) // 特殊处理：相等时 ppb 也要右移
            ppb++;
        ppa++;
    }
    else
    {
        C.insert(C.size(), B.get(ppb));
        ppb++;
    }
}
if (ppa == n) // ppa 出界
    for (int i = ppb; i < m; i++)
        C.insert(C.size(), B.get(i));
else // ppb 出界
    for (int i = ppa; i < n; i++)
        C.insert(C.size(), A.get(i));

std::cout << "合并结果：";
C.traverse();
return 0;

分析该时间复杂度，最后我们也只遍历了 $n+m$ 个元素，其他 get() 和 insert() 操作的时间复杂度均为 O(1)， 故最后的时间复杂度为 $O(n+m)$，简直是质的飞跃，可喜可贺！

上面展示了顺式存储的方式，链式存储的方式逻辑上与顺式存储一致，仅写法上有所差别，此处不再赘述。

递归

“To Iterate is Human, to Recurse, Divine.”
人理解迭代，神理解递归。

——L.Peter Deutsch

教材在完成栈的教学后引入了递归，这是合理的，但也是不合理的：递归的知识点和理解难度和栈完全不是一个等级，甚至可以说我可以为此新写一本《宝宝的第一本递归说明书》，因为栈是一种数据结构，排序是一种算法，而递归可以说是一种“思想”，所有和思想沾边的词语都代表着“渗透在程序的角落”。当然了，递归也没那么可怕，让我们先来看一个笑话：

人问神：“什么是递归？”

神说：“你要了解什么是递归，就先要知道什么是递归。”

这个笑话点出了递归的精髓：“自己调用自己”，就像是神说“什么是递归”的超链接链接到了人的问题，而下一步马上又来到了神的回答一样。但这并不是一个优美的递归，因为它成为了一个死循环，在这个笑话中没有退出的条件。我们可以再讲一个笑话：

从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：

“从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：

“从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：“有完没完不讲了！”。于是小和尚去睡觉了。”

于是小和尚去睡觉了。”

于是小和尚去睡觉了。

在这个笑话中，结束的条件就是老和尚说的话不再以“从前有座山”开头，即不再调用自身，而是说“有完没完不讲了”，那么小和尚去睡觉作为老和尚讲完故事的结尾，自然也就继续接在前面老和尚讲的故事后面。

欸……可是这样的话，好像跟循环有点像？你可能会有这样的疑问。虽然都是不断重复，但是循环是没有“调用自身”的过程的。或者说，上面那个笑话如果变成循环笑话就不成立，因为只是讲了三遍而已。我们再用一个例子来解释递归和循环的区别：

循环：你现在在一条走廊，走廊上有许多平行的门（就像是酒店一样），你的怪癖是打开门之后要跳一套广播体操，于是你进入第一扇门，跳一套广播体操，退出来；进入第二扇门，跳一套广播体操，退出来……；当门全部开完（或者其他结束条件）之后，你已经和第一扇门离得很远了。

递归：你现在打开了一扇门，进去，刚想跳广播体操，发现欸居然还有一扇门，然后你再进去，刚想跳广播体操，欸怎么还有一扇门……一直到最后，你发现门后没有门了，你跳了一套广播体操，退出来，想起来开门之后要跳广播体操呢，跳一下；退出来，跳一下……一直到最后，你回到了第一扇门。

现在你知道了递归和循环的差别。但是，呃，有什么区别吗？递归是用来解决什么问题的？

递归的基本思想

递归的基本思想正如它的名字：有“递”，有“归”——有“来”，有“回”。

我们以阶乘函数演示，$f(i)$ 表示 $i!$，它在数学中是这样表示的：

$$
f(x) = \begin{cases} 1 &,x=1 \\ xf(x-1) &,x \geq 2 \end{cases}
$$

发现了吗，在 $x \geq 2$ 的情况下，比方说我们要求 $f(3)$，对照函数，$f(3) = 3 \times f(2)$，那么我们又要知道 $f(2)$ 是什么……这就是一种递归。它重复调用了 $f(x)$ 这个函数，一直到 $f(1) = 1$ 这个确定的值，我不用再继续调用了，就可以往回代入了。我们以程序的写法来表示这个函数：

int fun(int x)
{
    if (x == 1)
        return 1;
    return x * fun(x - 1);
}

以 fun(6) 为例，分析这个过程：

递归演示

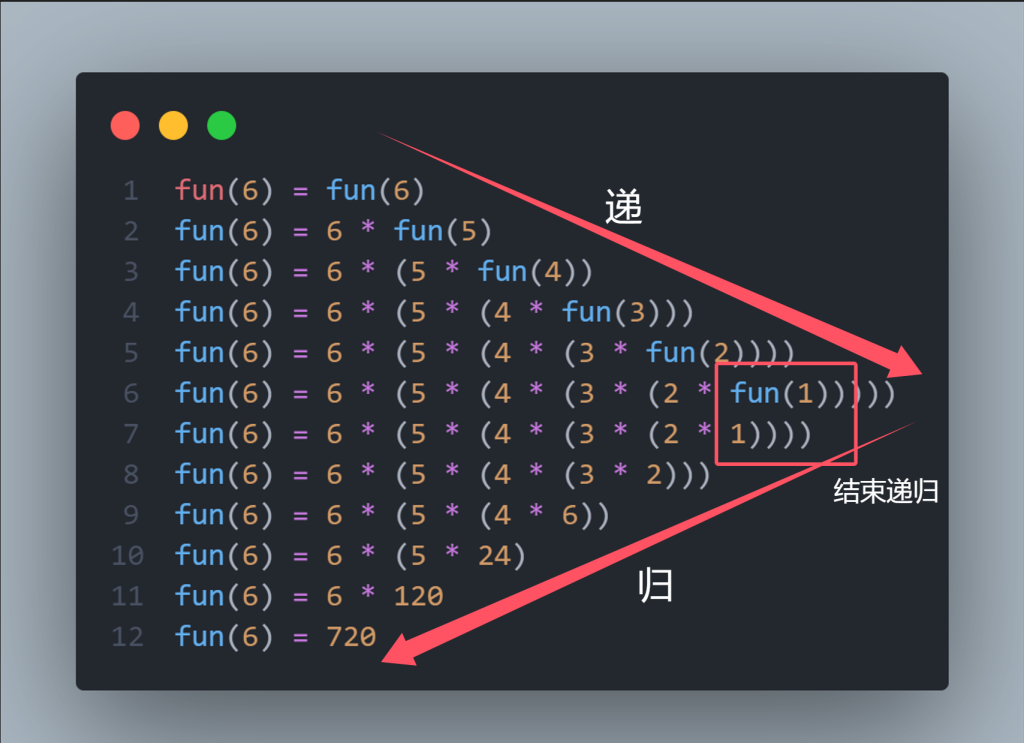
可见，我们把大问题（求解 fun(6)）不断分解成小问题（求解 fun(5)、fun(4)、……、fun(1)）的过程，叫做“递”；而把小问题的答案不断回代的过程叫做“归”。有递有归，才叫递归。

因此，我们不难发现递归过程中我们需要思考和解决的三个问题：

  1. 递的过程：我该如何把大问题分解成小问题？
  2. 归的过程：小问题的答案得到之后，我该如何回代回去？
  3. 递归终止：在什么时候应该结束递归？

递归问题演示

我们可以把递归问题分为三类：

  • 题目本身就以递归的形式提出。例如刚才说的递归问题。
  • 题目的内核需要递归的思想。例如等下会给出的经典汉诺塔问题。
  • 题目的结构是递归的

题目本身就以递归的形式提出

阶乘

设计一个函数求 $x!$

显然其终止条件应该是 $x = 1$ 时 $f(x) = f(1) = 1$ 恒成立，此时可以将函数值回代。

int fun(int x)
{
    if (x == 1)
        return 1;
    return x * fun(x - 1);
}

为了对比，下面展示常规循环解法：

int fun(int x)
{
    int res = 1; // 存储结果
    for (int i = 1; i <= x; i++)
        res *= i;
    return res;
}

循环解法实际上是利用

$$
x! = \prod_{i=1}^x i
$$

来设计函数。而递归解法实际上是利用

$$
f(x) = \begin{cases} 1 &,x=1 \\ xf(x-1) &,x \geq 2 \end{cases}
$$

来设计函数。

斐波那契数列

斐波那契数列指的是这么一个数列：

$$
1,1,2,3,5,8,13,21,\cdots
$$

除了第一项和第二项为 $1$ 之外，其余每一项都是前两项之和。在数学上，斐波那契数列也以这种方式定义：

$$
f(x) = \begin{cases} 1 &,x = 1 或x=2 \\ f(x-1) + f(x-2) &,x \geq 3 \end{cases}
$$

设计一个函数求斐波那契数列的任意一项。

普通递归解法

显然其终止条件和阶乘类似，是 $x = 1$ 或 $x = 2$ 时 $f(x) = 1$。即：

int fun(int x)
{
    if (x == 1 || x == 2)
        return 1;
    return fun(x - 1) + fun(x - 2);
}

我们发现，计算 $f(5)$，就要计算 $f(4)$ 和 $f(3)$，但计算 $f(4)$ 的时候，我们要计算 $f(3)$ 和 $f(2)$……我们又计算了一次 $f(3)$！当 $x$ 越大的时候，这个重复计算的劣势就会被无限放大……

计算这个函数的时间复杂度需要应用到之后树的知识，不过我们现在可以先给出：是 $O(2^N)$！这是一个很大的数字。

优化递归写法

还能不能优化？我们能不能把每一项只计算一次就得到结果？

我们选取斐波那契数列的前几项：

$$
1,1,2,3,5
$$

如果我们将其分成两个一组，可以得到

$$
\begin{align} f(1,1,3) = 2 \\ f(1,1,4) = 3 \\ f(1,1,5) = 5 \\ \end{align}
$$

其中，$f(1,1)$ 表示此刻以 $(1,1)$ 为一组，第三位表示以 $(1,1)$ 为数列开头的第几位。同理地

$$
\begin{align} f(1,2,3) = 3 \\ f(1,2,4) = 5 \\ \end{align}
$$

又

$$
f(2,3,3) = 5
$$

可见，

$$
f(1,1,5) = f(1,2,4) = f(2,3,3) = 5
$$

我们发现，$f(2,3,3) = 5$，刚好就能得到 $2 + 3 = 5$。——这个逻辑也很显然，以 $(2,3)$ 为开头的数列，其第三项不就是这两项的和吗？让我们尝试总结这个规律：

$$
f(a,b,n) = \begin{cases} 1 &,n=1 或 n = 2 \\ a + b &,n=3 \\ f(b,a+b,n-1) &,n \geq 4 \end{cases}
$$

可以写出代码：

int fun(int a, int b, int n)
{
    if (n == 1 || n == 2)
        return 1;
    else if (n == 3)
        return a + b;
    else
        return fun(b, a + b, n - 1);
}
记忆化递归写法

其实我们也有一种思路：既然我们想每一项都只算一次，那我存起来不就好了吗！每次需要用的时候，如果还没算过，就计算完之后存储起来；如果曾经算过了，就直接调用就好。这种写法叫做“记忆化”。配合递归，就叫“记忆化递归”。这样的写法还有一个好处：如果我们需要大量地调用斐波那契数列中的某一项，之后我们只要直接取用即可，无需重复计算。

我们用一个数组 memo[] 来存储 fun(x) 的结果，memo[i] 就表示 f[i] 的值。

const int maxN = 10000; // 提前规定好的最大值，假设为 10000

int memo[maxN];        // 记忆化存储斐波那契数列的值
memo[1] = memo[2] = 1; // 提前初始化

int fun(int x)
{
    if (memo[x])                              // 如果曾经存储过
        return memo[x];                       // 直接调用
    return memo[x] = fun(x - 1) + fun(x - 2); // 否则计算之后存储起来
}

这样，原递归写法的时间复杂度就降为 $O(N)$ 了。当然了，虽然用处不大，但是你也可以将其中递归的方法替换为我们优化后的算法：

const int maxN = 10000; // 提前规定好的最大值，假设为 10000

int memo[maxN];        // 记忆化存储斐波那契数列的值
memo[1] = memo[2] = 1; // 提前初始化

int fun(int a, int b, int n)
{
    if (memo[n])        // 如果曾经存储过
        return memo[n]; // 直接调用
    else if (n == 3)
        return memo[n] = a + b;
    return memo[n] = fun(b, a + b, n - 1);
}
循环写法

以上写法的空间复杂度都是 $O(N)$（你也许不会算，但没关系）。其中普通递归写法调用了栈（这是我们等下要讲的），记忆化递归写法同时还生成了一个数组……能不能只用变量完成这一切？

我们这次把三个数看成一组，分别记为 first、second 和 result，显然有

first + second = result

而接下来移动到下一轮，我们发现 result 此时变为了 second，second 变成了 first……就这样不断循环下去，我们就可以最终计算出我们需要的斐波那契数列的值。

下面给出代码：

int result = 0;
int first = 1, second = 1; // 初始化

int fun(int x)
{
    if (x == 1 || x == 2)
        return 1; // 特判
    for (int i = 3; i <= x; i++)
    {
        result = first + second;
        first = second;
        second = result;
    }
    return result;
}

尽管时间复杂度也为 $O(N)$，但空间复杂度降为 $O(1)$，是我们目前能理解的最优秀的算法，但比较难以理解。可见，递归并不是优于其他的算法，而是得益于在解决部分问题的时候思路更清晰，而且代码非常的简短优美。

第一类问题总结

这一类问题本身就可以用“递归”的思想解决，它们表现为可以重复调用自身，或者是大问题显然和自身的子问题相关。其他的第一类问题还有杨辉三角（我不想画图了）、判断回文字符串和字符串全排列（我们还没讲到字符串）、二分查找（我们还没讲到查找）等等。我们之后或许还会遇到。

题目的内核需要递归的思想

汉诺塔问题

汉诺塔问题是一个研究透得不能再透了的问题。情景千奇百怪，但大致如下：

古代有一个梵塔，塔内有三个座 $A、B、C$，$A$ 座上有 $64$ 个盘子，盘子大小不等，大的在下，小的在上。有一个和尚想把这 $64$ 个盘子从 $A$ 座移到 $C$ 座，但每次只能允许移动一个盘子，并且在移动过程中，$3$ 个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用 $B$ 座。要求输入层数，运算后输出每步是如何移动的。

汉诺塔演示（图片来源于 CSDN @xhhh113，侵删）

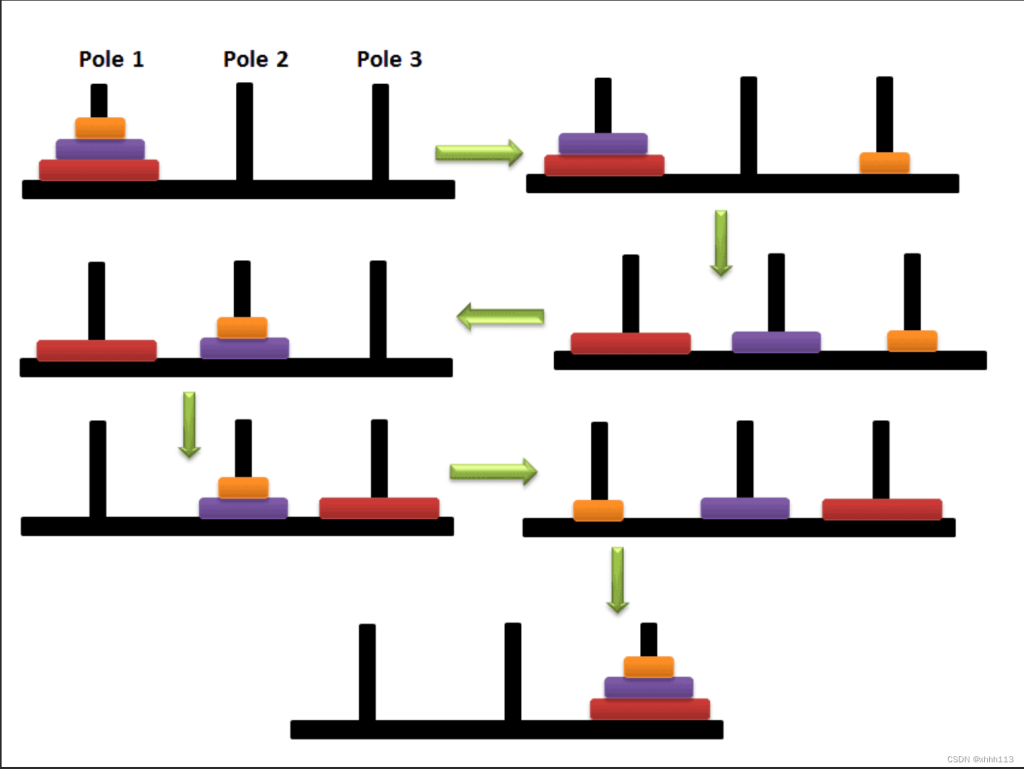
尝试分析这个问题……等等，怎么分析？这可是 $64$ 个盘子！当一个问题的规模有点大时，我们就应该想想是否可以缩小问题。如果只有一个盘子的话，情况是：

ABC
1
1

如果只有两个盘子的话，情况应该是这样的（左右表示上下次序）：

ABC
1 2
21
12
1 2

完美！参照上图，我们写出三个的情况：

ABC
1 2 3
2 31
321
31 2
1 23
123
12 3
1 2 3

同样非常完美！但是好像情况变得有点复杂了……可是注意看，当第三个盘子已经放到 $C$ 的时候，情况实际上回到了两个盘子的时候——因为小的可以放在大的上面，所以当放小盘子的时候，所有比它大的盘子对它来说都是可以放置的空位。那么只要我们把当前最大的盘子放在 $C$，那么情况就变成了当前盘子数 $-1$ 的情况。这样，问题就被不断缩小了。

有点抽象？让我们再总结一下这个过程，它分成三个步骤：

  1. 将最大的盘子上面所有的盘子（$63$ 个）放在 $B$ 上
  2. 将最大的盘子放在 $C$ 上
  3. 将剩下的盘子放在 $C$ 上

什么，你说一次只能移动一个盘子？我们把上面所有的盘子看成一个不就好了吗？至于接下来怎么操作，我们再只看这 $63$ 个盘子，把上面 $62$ 个看成整体……如此往复，最后变成只有一个盘子的情况。可以参考上图。这个过程和递归的思想不谋而合，下面给出代码：

#include <iostream>

using namespace std;

// 汉诺塔问题解决程序
// level 表示第 level 号盘子，from/to 分别表示盘子的来向和去向，
void solve(int level, char from, char inter, char to)
{
    if (level == 1) // 递归终止条件
        cout << "从 " << from << " 移动盘子 " << level << " 号到" << to << " \n";
    else
    {
        // 将 level-1 个盘子从 from 移到 inter
        solve(level - 1, from, to, inter);
        cout << "从 " << from << " 移动盘子 " << level << " 号到" << to << " \n";
        solve(level - 1, inter, from, to);
    }
}

int main()
{
    solve(3, 'A', 'B', 'C');
    return 0;
}

输出：

从 A 移动盘子 1 号到 C
从 A 移动盘子 2 号到 B
从 C 移动盘子 1 号到 B
从 A 移动盘子 3 号到 C
从 B 移动盘子 1 号到 A
从 B 移动盘子 2 号到 C
从 A 移动盘子 1 号到 C

题目的结构是递归的

这种问题的典型是我们之后会学习的二叉树。这里先不赘述。同时，链表的遍历也可以递归地处理，这是因为链表的节点结构：

struct Node
{
    T data;
    Node *next;
    Node(const T &data) : data(data), next(nullptr) {}
};

其中，Node 种指向下一个节点的指针 *next 的结构定义同样是 Node，即其结构定义又调用了自身，符合递归的定义。我们原本的链表遍历写法是：

// 遍历表
template <typename T>
void linkedList<T>::traverse() const
{
    node *cur = head;
    while (cur)
    {
        std::cout << cur->data << " ";
        cur = cur->next;
    }
    std::cout << std::endl;
}

我们可以将其改写为：

// 遍历表（递归形式）
template <typename T>
void linkedList<T>::traverse(Node *p) const
{
    if (p == nullptr)
        return; // 递归终止条件
    else
    {
        std::cout << p->data << " ";
        traverse(p->next);
    }
    std::cout << std::endl;
}

递归和栈的关系

所以为什么递归要放在栈中讲？

在阐述它们之间的关系之前，先了解到一个计算机的基本原理：程序执行一个函数时，就会创建一个受保护的独立空间（新的函数栈）。我们知道每个函数的局部变量都是独立的，就是因为它们是在这个新空间中被创建的。我们以求阶乘的例子说明这个过程：

int fun(int x)
{
    if (x == 1)
        return 1;
    return x * fun(x - 1);
}

画图：

递归栈演示

可见，每次运行调用一次函数，就会在这个栈上加一层。如果调用的次数过多，超出了这个栈的大小，那么就会“爆栈”，我们称之为栈溢出 StackOverflow。正因如此，调用的次数（我们称之为深度）不能太深，通常在 $6 \times 10^4$ 以上就会出现爆栈的情况。

递归的时间复杂度

我们前面曾经提到过递归程序的时间复杂度。这里我们直接放弃复杂的推导和严谨的计算，直接给出结论：

$$
递归的时间复杂度 = 调用的次数 \times 一次调用的时间复杂度
$$

例如，对于阶乘：

int fun(int x)
{
    if (x == 1)
        return 1;
    return x * fun(x - 1);
}

每次调用的时候的操作都是 $O(1)$ 的，过程中调用 $x$ 次，故时间复杂度为 $O(N)$。

再如斐波那契数列的普通递归写法：

int fun(int x)
{
    if (x == 1 || x == 2)
        return 1;
    return fun(x - 1) + fun(x - 2);
}

每次调用的时候的操作都是 $O(1)$ 的，但每次 return 的时候都要重复调用自身 2 次，求 fun(x) 的过程中就要调用 $2^x$ 次，故时间复杂度为 $O(2^N)$。

串

在 C 语言的学习中，我们称 "Hello,world!" 是一个字符串。那么字符串，其实也就简称为串。它和我们所熟知的线性表（即顺序表 / 链表）类似，但它存储的每一个元素只能是字符。

如果仅仅只是这样的话，那么我们就没有什么好额外研究它的必要了。研究字符串和普通线性表最大的不同点是，我们一般来说会研究字符串的整体或整体的部分，而不会研究单独里面的某一个字符。例如，对于 "applepen"，我们可能比较关心它其实是由 apple 和 pen 两个字符串组合起来的，而不是“这个字符串的第一个字母是 a”。

所以，哒哒——为了研究全都是字符的线性表，以及它更倾向于研究整体的特点，我们创造出了字符串。

我们参考书上的一些字符串常用操作，给出字符串类的定义文件：

定义（myString.h）

#ifndef MY_STRING_H
#define MY_STRING_H

#include <iostream>
#include <stdexcept>

class myString
{
private:
    char *data;
    size_t length; // 字符串长度

    // 辅助函数：用于计算字符串的长度
    size_t cal_length(const char *str) const const;

    // 辅助函数：用于复制字符串
    void copyString(char *dest, const char *src, size_t len) const;

public:
    // 构造函数，初始化字符串，可以接收 C 语言风格字符串
    myString(const char *str = "");

    // 复制构造函数
    myString(const myString &other);

    // 析构函数
    ~myString();

    // 赋值运算符重载
    myString &operator=(const myString &other);

    // 检查字符串是否为空
    bool isEmpty() const;

    // 获取字符串长度
    size_t size() const;

    // 清空字符串
    void clear();

    // 字符串连接的运算符重载
    myString &operator+(const myString &other) const;

    // 获取从 pos 开始长度为 len 的子串
    myString subString(size_t pos, size_t len) const;

    // 查找 pos 位置开始模式串 pattern 在字符串中的位置
    size_t find(const myString &pattern, size_t pos = 0);

    // 用另一字符串替换所有与模式串相等的不重叠子串
    myString replace(const myString &pattern, const myString &replacement) const;

    // 在 pos 位置插入字符串
    myString insert(size_t pos, const myString &str) const;

    // 删除从 pos 位置起指定长度子串
    myString erase(size_t pos, size_t len) const;

    // 重载用于输出字符串的友元函数
    friend std::ostream &operator<<(std::ostream &os, const myString &str);

    // 比较运算符重载
    bool operator==(const myString &other) const;
    bool operator!=(const myString &other) const;
    bool operator<(const myString &other) const;
    bool operator<=(const myString &other) const;
    bool operator>(const myString &other) const;
    bool operator>=(const myString &other) const;
};

#endif // MY_STRING_H

实现（myString.cpp）

字符串的函数实现比较复杂，下面解释一些个别函数的实现。

（复制）构造函数

该函数的作用是接收 C 语言风格与该字符串类相同的字符串并将其转化。

// 构造函数，初始化字符串，可以接收 C 语言风格字符串
myString::myString(const char *str = "")
{
    if (!str)
        throw std::invalid_argument("目标非字符串");
    length = cal_length(str);
    data = new (std::nothrow) char[length + 1]; // std::nothrow 表示分配失败时返回一个空指针 nullptr
    if (!data)
        throw std::bad_alloc();    // 分配失败
    copyString(data, str, length); // 复制字符串
}

// 复制构造函数
myString::myString(const myString &other)
{
    length = other.length;
    data = new (std::nothrow) char[length + 1];
    if (!data)
        throw std::bad_alloc();
    copyString(data, other.data, length);
}

值得解释的是，在构造函数中的

 throw std::invalid_argument("目标非字符串");

是异常处理，表示此时的输入有错误。此处及下文类似的异常处理都是为了提高程序的健壮性。

 data = new (std::nothrow) char[length + 1]; // std::nothrow 表示分配失败时返回一个空指针 nullptr

此处是为新的字符串新建一个字符数组空间，length + 1 是在字符串长度的基础上补充一个 ‘\0’ 作为字符串的结尾。std::nothrow 表示分配失败时返回一个空指针 nullptr，即是为了下面的异常处理：

 if (!data)
     throw std::bad_alloc();

当分配失败时返回空指针，即此时抛出分配失败的异常。如果成功，那么执行字符串拷贝函数。

赋值运算符重载

这里运用到了等号（赋值）运算符重载的知识。当你对类对象进行赋值运算符（=）时，如果没有自己定义赋值操作符的重载函数，编译器会生成一个默认的赋值运算符重载函数，而这个赋值运算符是浅拷贝的。

浅拷贝的意思是只是简单地将一个对象的内存数据复制到另一个对象。这意味着如果对象的成员变量是指针或者引用外部资源（例如通过 new 动态分配的内存），那么两个对象的成员变量都将指向同一个内存。

而如果两个对象共享一块内存，当其中一个对象的生命周期结束并调用析构函数时，这块内存会被释放。如果另一个对象随后也尝试释放这块内存（因为它也指向这一块内存），就会导致程序崩溃，因为同一块内存被释放了两次。

为了解决这个问题，通常需要自己定义赋值运算符的重载函数，这个操作叫深拷贝。深拷贝会为每个对象分配独立的内存空间，从而避免多个对象共享同一块内存。

// 赋值运算符重载
myString &myString::operator=(const myString &other)
{
    if (this != &other)
    {
        delete[] data; // 释放旧内存
        length = other.length;
        data = new (std::nothrow) char[length + 1];
        if (!data)
            throw std::bad_alloc();
        copyString(data, other.data, length);
    }
    return *this;
}

赋值运算符重载一般分成三个过程：

释放旧的内存，对应

 delete[] data; // 释放旧内存

分配新的内存大小，对应

 length = other.length;
 data = new (std::nothrow) char[length + 1];
 if (!data)
     throw std::bad_alloc();

重新赋值，对应

 copyString(data, other.data, length);
 return *this;
连接（+）运算符重载

为了方便地连接两个字符串，我们可以重载 + 运算符。这个过程实际上是新建一块大小等于两个字符串长度和的字符数组，并在两段分别执行复制操作。

 // 字符串连接的运算符重载
 myString myString::operator+(const myString& other) const
 {
     size_t new_length = length + other.length;
     char* newData = new (std::nothrow) char[new_length + 1];
     if (!newData)
         throw std::bad_alloc();
     copyString(newData, data, length);
     copyString(newData + length, other.data, other.length); // 地址增加 length
     myString result(newData);
     return result;
 }
获取某位置起一定长度的子串

首先给出获取子串的代码：

// 获取从 pos 开始长度为 len 的子串
myString myString::subString(size_t pos, size_t len) const
{
    if (pos > length)
        throw std::out_of_range("索引非法");
    size_t new_length = (pos + len > length) ? length - pos : len;
    char* subData = new (std::nothrow) char[new_length + 1];
    if (!subData)
        throw std::bad_alloc();
    for (size_t i = 0; i < new_length; i++)
        subData[i] = data[pos + i];
    subData[new_length] = '\0';
    return myString(subData);
}

值得注意的是返回的字符串的长度判断，它在程序中表现为：

 size_t new_length = (pos + len > length) ? length - pos : len;

即如果子串的长度已经超过了主串剩下的长度，即 pos + len > length，那么显然子串也只能为剩下那一段，即长度为 length - pos。

查找从某位置起模式串在主串中的位置

我们只要运用最朴素的暴力思想，从某位置起，按位对比，如果出现了模式串，那么就可以返回这个位置，即是需要的答案。

 // 查找 pos 位置开始模式串 pattern 在字符串中的位置
 size_t myString::find(const myString& pattern, size_t pos) const
 {
     for (size_t i = pos; i <= length - pattern.length; i++)
     {
         size_t j = 0;
         while (j < pattern.length && data[i + j] == pattern.data[j])
             j++;
         if (j == pattern.length)
             return i;
     }
     return static_cast<size_t>(-1);
 }
用另一字符串替换所有与模式串相等的不重叠子串
// 用另一字符串替换所有与模式串相等的不重叠子串
myString myString::replace(const myString& pattern, const myString& replacement)
{
    myString res;
    size_t pos = 0, lastPos = 0;
    while ((pos = find(pattern, lastPos)) != static_cast<size_t>(-1))
    {
        res = res + subString(lastPos, pos - lastPos) + replacement;
        lastPos = pos + pattern.length;
    }
    res = res + subString(lastPos, length - lastPos);
    return res;
}

其中，pos 和 lastpos 表示需要替换的模式串开始和结束字符串的位置。同时：

 (pos = find(pattern, lastPos)) != static_cast<size_t>(-1)

表示更新 pos 为从上一个需要替换的字符串结尾的下一位开始寻找新的模式串的位置。static_cast<size_t>(-1) 表示到不存在的位置。

 res = res + subString(lastPos, pos - lastPos) + replacement;

即为连接字符串，将前面的字符串、改写前的字符串和改变之后的字符串连接在一起。

重载插入运算符 <<
// 重载用于输出字符串的函数
std::ostream &operator<<(std::ostream &os, const myString &str)
{
    os << str.data;
    return os;
}

这是重载了插入运算符，cout 是 ostream 的对象。ostream 和 cout 都是在头文件 <iostream> 中被声明的。我们可以重载该插入运算符，使得我们可以通过 std::cout << 来输出我们的字符串类。其中 o 即为 out，输出的意思。

各种比较运算符重载
各种比较运算符重载

字符串的比较遵从这么一个原则：两个字符串逐位比较，ASCII 码较大的字符串就较大，若相等则继续比较下一位。如果可比较的字符都比较完了，长度较长的字符串就较大。详细来说，对于两个字符串 str1 和 str2，比较规则为：

  • 从两个字符串的第 $0$ 个位置开始，依次比较对应位置上的字符 ASCII 码大小。
    • 如果该位置上，ASCII 码大小相等，则顺延比较下一位
    • 该位置上，谁的 ASCII 码大，该字符串就大
  • 如果比较到某一个字符串末尾，而另一个字符串仍有剩余，谁的长度大，字符串就大。

因此，两个字符串相等的条件是：

  • 长度相等
  • 对应位置上的字符（ASCII 码）都相同

我们可以先重载 == 等于运算符：

 // 比较运算符重载
 bool myString::operator==(const myString &other) const
 {
     if (length != other.length)
         return false;
     for (size_t i = 0; i < length; i++)
         if (data[i] != other.data[i])
             return false;
     return true;
 }

就可以写出 != 的重载：

bool myString::operator!=(const myString &other) const
{
    return !(*this == other);
}

同理地，我们可以重载 <：

 bool myString::operator<(const myString &other) const
 {
     size_t min_length = length < other.length ? length : other.length;
     for (size_t i = 0; i < min_length; i++)
     {
         if (data[i] < other.data[i])
             return true;
         if (data[i] > other.data[i])
             return false;
     }
     return length < other.length;
 }

就可以利用逻辑顺便把其他的运算符重载了：

bool myString::operator<=(const myString &other) const
{
    return *this < other || *this == other;
}

bool myString::operator>(const myString &other) const
{
    return !(*this <= other);
}

bool myString::operator>=(const myString &other) const
{
    return !(*this < other);
}
完整代码
#include "myString.h"

// 辅助函数：用于计算字符串的长度
size_t myString::cal_length(const char *str) const
{
    size_t len = 0;
    while (str[len] != '\0')
        len++;
    return len;
}

// 辅助函数：用于复制字符串
void myString::copyString(char *dest, const char *src, size_t len) const
{
    for (size_t i = 0; i < len; i++)
        dest[i] = src[i];
    dest[len] = '\0';
}

// 构造函数，初始化字符串，可以接收 C 语言风格字符串
myString::myString(const char *str)
{
    if (!str)
        throw std::invalid_argument("目标非字符串");
    length = cal_length(str);
    data = new (std::nothrow) char[length + 1]; // std::nothrow 表示分配失败时返回一个空指针 nullptr
    if (!data)
        throw std::bad_alloc();    // 分配失败
    copyString(data, str, length); // 复制字符串
}

// 复制构造函数
myString::myString(const myString &other)
{
    length = other.length;
    data = new (std::nothrow) char[length + 1];
    if (!data)
        throw std::bad_alloc();
    copyString(data, other.data, length);
}

// 析构函数
myString::~myString()
{
    delete[] data;
}

// 赋值运算符重载
myString &myString::operator=(const myString &other)
{
    if (this != &other)
    {
        delete[] data; // 释放旧内存
        length = other.length;
        data = new (std::nothrow) char[length + 1];
        if (!data)
            throw std::bad_alloc();
        copyString(data, other.data, length);
    }
    return *this;
}

// 检查字符串是否为空
bool myString::isEmpty() const
{
    return length == 0;
}

// 获取字符串长度
size_t myString::size() const
{
    return length;
}

// 清空字符串
void myString::clear()
{
    delete[] data;
    data = new (std::nothrow) char[1];
    if (!data)
        throw std::bad_alloc();
    data[0] = '\0';
    length = 0;
}

// 字符串连接的运算符重载
myString myString::operator+(const myString &other) const
{
    size_t new_length = length + other.length;
    char *newData = new (std::nothrow) char[new_length + 1];
    if (!newData)
        throw std::bad_alloc();
    copyString(newData, data, length);
    copyString(newData + length, other.data, other.length); // 地址增加 length
    myString result(newData);
    return result;
}

// 获取从 pos 开始长度为 len 的子串
myString myString::subString(size_t pos, size_t len) const
{
    if (pos > length)
        throw std::out_of_range("索引非法");
    size_t new_length = (pos + len > length) ? length - pos : len;
    char *subData = new (std::nothrow) char[new_length + 1];
    if (!subData)
        throw std::bad_alloc();
    for (size_t i = 0; i < new_length; i++)
        subData[i] = data[pos + i];
    subData[new_length] = '\0';
    return myString(subData);
}

// 查找 pos 位置开始模式串 pattern 在字符串中的位置
size_t myString::find(const myString &pattern, size_t pos) const
{
    for (size_t i = pos; i <= length - pattern.length; i++)
    {
        size_t j = 0;
        while (j < pattern.length && data[i + j] == pattern.data[j])
            j++;
        if (j == pattern.length)
            return i;
    }
    return static_cast<size_t>(-1);
}

// 用另一字符串替换所有与模式串相等的不重叠子串
myString myString::replace(const myString &pattern, const myString &replacement)
{
    myString res;
    size_t pos = 0, lastPos = 0;
    while ((pos = find(pattern, lastPos)) != static_cast<size_t>(-1))
    {
        res = res + subString(lastPos, pos - lastPos) + replacement;
        lastPos = pos + pattern.length;
    }
    res = res + subString(lastPos, length - lastPos);
    return res;
}

// 在 pos 位置插入字符串
myString myString::insert(size_t pos, const myString &str) const
{
    if (pos > length)
        pos = length;
    return subString(0, pos) + str + subString(pos, length - pos);
}

// 删除从 pos 位置起指定长度子串
myString myString::erase(size_t pos, size_t len) const
{
    if (pos >= length)
        throw std::out_of_range("索引非法");
    size_t new_length = (pos + len > length) ? length - pos : len;
    return subString(0, pos) + subString(pos + new_length, length - pos - new_length);
}

// 重载用于输出字符串的函数
std::ostream &operator<<(std::ostream &os, const myString &str)
{
    os << str.data;
    return os;
}

// 比较运算符重载
bool myString::operator==(const myString &other) const
{
    if (length != other.length)
        return false;
    for (size_t i = 0; i < length; i++)
        if (data[i] != other.data[i])
            return false;
    return true;
}

bool myString::operator!=(const myString &other) const
{
    return !(*this == other);
}

bool myString::operator<(const myString &other) const
{
    size_t min_length = length < other.length ? length : other.length;
    for (size_t i = 0; i < min_length; i++)
    {
        if (data[i] < other.data[i])
            return true;
        if (data[i] > other.data[i])
            return false;
    }
    return length < other.length;
}

bool myString::operator<=(const myString &other) const
{
    return *this < other || *this == other;
}

bool myString::operator>(const myString &other) const
{
    return !(*this <= other);
}

bool myString::operator>=(const myString &other) const
{
    return !(*this < other);
}

数组

数组是我们大家都非常熟悉的老朋友了。唯一需要补充的内容是对于特殊矩阵的压缩存储——利用较少的存储空间存储这个矩阵的信息。

对称矩阵

若对一个 $n$ 阶矩阵 $A$ 中的任意一个元素 $a_{i,j}$ 都有 $a_{i,j} = a_{j,i}\,(1 \leq i,j \leq n)$，则称其为对称矩阵。其中的元素可以划分为三个部分，即上三角区、主对角线和下三角区。

对称矩阵演示

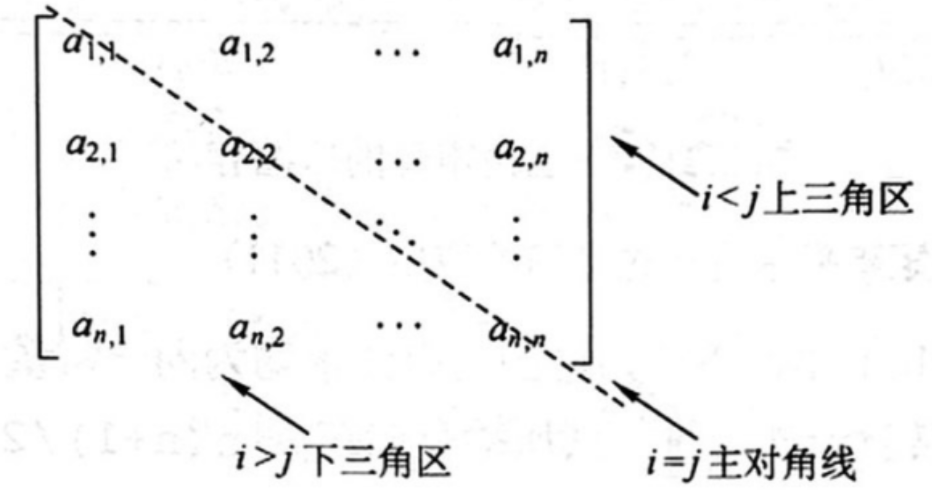
空间大小

对称矩阵的上三角区的所有元素和下三角区的对应元素相同。我们可以只存放上/下三角部分和主对角线部分的元素。存储的空间大小为

$$
1 + 2 + \cdots + n = \dfrac{n(n+1)}{2}
$$

行列坐标和数组元素下标的关系

矩阵元素 $a_{i,j}$ 的行号 $i$ 和列号 $j$ 通常是从 $1$ 开始的，而数组元素 b[k] 的下标 $k$ 通常是从 $0$ 开始的。假设存放下三角区和主对角线的部分，那么位于元素 $a_{i,j}\,(i \geq j)$ 前面的元素有

$$
a_{1,1},a_{2,1},a_{2,2},\cdots,a_{i-1,1},a_{i-1,2},\cdots,a_{i-1,i-1},a_{i,1},a_{i,2},\cdots,a_{i,j-1}
$$

共

$$
1 + 2 + \cdots + (i-1) + j – 1 = \dfrac{i(i-1)}{2} + j – 1
$$

由于上三角区与下三角区完全对应，只要交换 $i,j$ 即可。最终得到：

$$
k = \begin{cases} \dfrac{i(i-1)}{2} + j – 1 &,i \geq j \\ \dfrac{j(j-1)}{2} + i – 1 &,i < j \\ \end{cases}
$$

下面给出了从下标从 $1$ 或者从 $0$ 开始的其他可能。

矩阵从 1 开始，数组从 1 开始

$$
k = \begin{cases} \dfrac{i(i-1)}{2} + j &,i \geq j \\ \dfrac{j(j-1)}{2} + i &,i < j \\ \end{cases}
$$

矩阵从 0 开始，数组从 0 开始

$$
k = \begin{cases} \dfrac{i(i+1)}{2} + j &,i \geq j \\ \dfrac{j(j+1)}{2} + i &,i < j \\ \end{cases}
$$

矩阵从 0 开始，数组从 1 开始

$$
k = \begin{cases} \dfrac{i(i+1)}{2} + j + 1 &,i \geq j \\ \dfrac{j(j+1)}{2} + i + 1 &,i < j \\ \end{cases}
$$

三角矩阵

三角矩阵分成下三角矩阵、上三角矩阵和对称矩阵。对于 $n$ 阶矩阵 $A$ 来说：

  • 若当 $i< j$ 时，有 $a_{ij} = 0$，则称此矩阵为下三角矩阵。
  • 若当 $i > j$ 时，有 $a_{ij} = 0$，则称此矩阵为上三角矩阵。
  • 若矩阵中的所有元素均满足 $a_{ij} = a_{ji}$，则称此矩阵为对称矩阵。

分析过程与对称矩阵类似，下面直接给出公式。

矩阵从 1 开始，数组从 0 开始

$$
k = \begin{cases} \dfrac{i(i-1)}{2} + j – 1 &,i \geq j \\ \dfrac{n(n+1)}{2} &,i < j \\ \end{cases}
$$

矩阵从 1 开始，数组从 1 开始

$$
k = \begin{cases} \dfrac{i(i-1)}{2} + j &,i \geq j \\ \dfrac{n(n+1)}{2} &,i < j \\ \end{cases}
$$

矩阵从 0 开始，数组从 0 开始

$$
k = \begin{cases} \dfrac{i(i+1)}{2} + j &,i \geq j \\ \dfrac{n(n+1)}{2} &,i < j \\ \end{cases}
$$

矩阵从 0 开始，数组从 1 开始

$$

k =
\begin{cases}
\dfrac{i(i+1)}{2} + j + 1 &,i \geq j \
\dfrac{n(n+1)}{2} + 1 &,i < j \
\end{cases}


$$

2024.09.21
内容发布
2024.09.26
修正文章格式
修正了文章中部分数学公式 LaTex 渲染错误的问题。
修正了文章中部分前后引号位置错误的问题。
文章内容补充
在链表的类定义和实现中补充了头插法和尾插法构造数组的函数定义和实现。
2024.10.10
修正文章内容
修正了文章中部分代码问题。
2024.10.24
修正文章格式
将文章错误的标题层级修正。

作者

觉得有帮助的话可以投喂煮啵，助力煮啵过上点外卖不用神卷的生活

本文作者：Flaw_Owl
看到这里的朋友们，作者十分感谢！如果你看到任何写得不清楚或是错误之处，或者是有什么希望看到的课程和内容笔记，欢迎在评论区留言！评论区可以单纯的发表文字，也可以使用 Markdown 语法，你可以参照 Markdown 官方教程发出带有格式的评论。

版权说明：本博客所有文章除特别声明外，均采用CC BY-NC-SA 4.0协议，转载请注明文章地址及作者哦
暂无评论

发送评论 编辑评论




























|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
颜文字
Emoji
小恐龙
花!



上一篇
下一篇 


推荐文章
【宝宝的第一本数据结构】01 顺序表


【宝宝的第一本数据结构】05 树与二叉树


【宝宝的第一本数据结构】02 链表


【宝宝的第一本数据结构】03 栈和队列


【宝宝的第一本数据结构】00 前言


【数据结构作业】2024.09.26 头插法、尾插法创建单链表


【数据结构作业】2024.09.19 顺序表的实现