树与二叉树
本文图片主要来源于:07. 树 | 算法通关手册(LeetCode) (itcharge.cn)
箭头并非只能有一个
在前面的章节中,我们介绍了在卡片上画一个箭头,以此靠“虚拟的线”连接在一起的链表。每一张卡片上的箭头都指向下一张卡片。
但是……我们并没有说箭头只能画一个啊!如果一个卡片上可以有多个箭头指向其他的卡片,而这些被指向的卡片也可以继续画更多的箭头的话……会变成什么呢?
好吧,让我们先从一种比较简单的情况开始。在链表中,我们的箭头可以表述为“先后关系”,我们也将其称为“前驱”和“后继”。现在让我们规定:每一个节点都只有一个前驱,而可以有很多个后继;也就是说,对于每一张卡片,只有一个箭头指向它,而可以有无数个箭头指向其他卡片。
思考这种情况,其正如现实生活中的树一般:树只有一个根,而向上可以生长出无数的枝条;而如果将其中一个枝条看作“根”,它又可以继续生长出其他的枝条……
由此,我们将这种数据结构称之为“树”。
树
数据结构的树长这个样子:
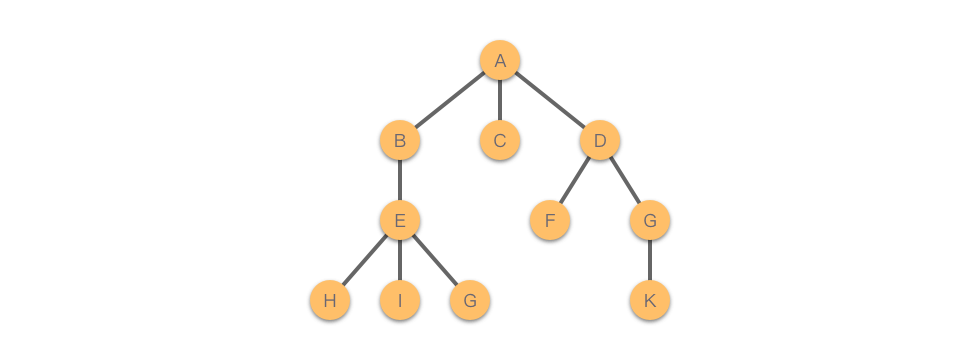
比起现实世界中的树来说,数据结构的树其实是一棵倒挂的树:根朝上,叶朝下。
书本上的严格定义是这样的:
由 $n \geq 0$ 个节点与节点之间的关系组成的有限集合。当 $n = 0$ 时称为空树,当 $n > 0$ 时称为非空树。
这是一个比较好理解的定义。节点就是我们前面说的卡片,这些关系就是我们前面说的箭头。我们前面规定过,在树这种数据结构中,我们让每一个节点都只有一个前驱,而可以有很多个后继。
特别地,其中有且只有一个节点没有前驱节点,这个节点就被称为根节点(Root)。如图中的节点 $A$。
我们前面又说,正如现实生活中的树一般,如果把每一根枝条都看作一个新的“根”的话,那么每一个枝条上都可以继续生长出其他的枝条。——也就是说,我们可以把这个新的“根”和在其上生长出来的其他枝条看作一棵新的“树”。那么有别于最开始的那棵树,这个树就叫做“子树(SubTree)”。
严格的定义是,除了根节点之外的其他节点,都可以分为几个互不相交的有限集合,每个集合本身都是一棵树,记作 $T_i$。如下图所示,红色节点 $A$ 是根节点,除了根节点之外,还有 $3$ 棵互不相交的子树 $T_1(B,E,H,I,G)$,$T_2(C)$,$T_3(D,F,G,K)$。
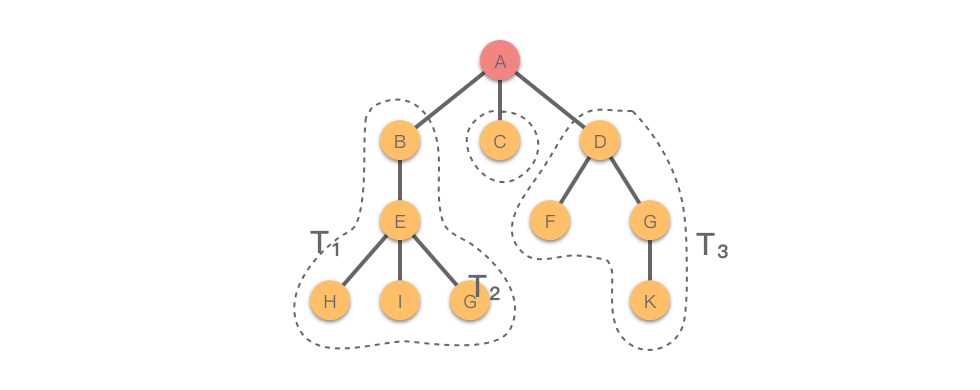
树的术语
现在你已经知道了树。但是和之前所有的数据结构一样,为了方便称呼而不是一直用比喻,计算机科学家们定义了一些比较抽象的概念。对于一棵树而言,我们要分析什么?我们可以从三个方面来分析:对于节点本身,对于连接在一起的节点,对于未连接在一起的节点。
节点本身
像上图一样,我们来看这三棵子树的根:其中 $B$ 之下只有一个分支,$C$ 之下没有分支,$D$ 之下有两个分支——其实分支也就是子树的个数。我们把这个概念称之为节点的度(Degree)。因此,$B,C,D$ 的度就分别是 $1,0,2$。
根据现实生活中的概念,度为 $0$ 的概念显然比较特殊:它没有任何的分支,也就是没有长出任何的枝条,我们就把这样的节点叫做叶子节点或者终端节点。
对应的,我们就把度不为 $0$ 的节点称之为分支节点或者非终端节点。
我们如何评价一棵树是茁壮还是矮小?很多时候我们会根据它是否“枝繁叶茂”,也就是说“它是否有很多的枝条”。反映到数据结构中,树中各节点的最大度数就会被称为树的度。

连接在一起的节点
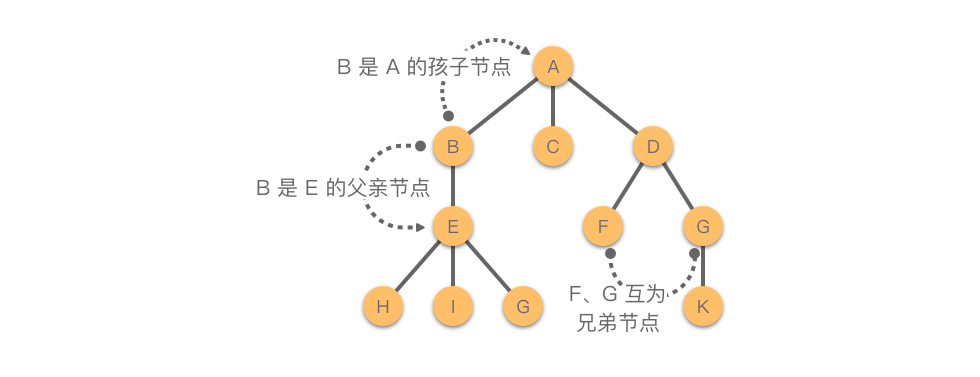
我们讨论完了卡片,现在就要来讨论箭头的问题了。我们说过,树的结构特点是除了根节点之外,每个节点都只有一个前驱,但可以有无数个后继。显然,如果一个节点有多个前驱的话,相当于有多个根同时长出了这个枝条,画面会变得比较诡异且不合逻辑。照应到现实生活中,家庭关系也和这个情况比较类似。在不考虑极端情况下,一个孩子只会有一个生物学父亲,但这个孩子如果选择生育,那么 TA 可以有很多个后代。因此,我们就把某个节点的前驱叫做它的父节点(父亲节点),相应的,这个节点就叫做其前驱的子节点(孩子节点)。某个节点可能有很多个后驱,这些后驱就互相称为兄弟节点。
为什么是“父节点”,而不是“母节点”?
从语言学的角度而言,“父”一般更多表达的是层级关系、继承(传递)和权限(控制)方面的概念,例如“父节点”、“父目录”、“父类”等。而“母”一般更多表达的是衍生关系、复制(生产)和承载(容纳)方面的概念,例如“航母”、“母带”、“母题”等。
从历史翻译的角度而言,过去的最早一批国外计算机科学家就是用 farther 和 son 来描述父节点和子节点的,因此当时的中文翻译教材也就这样翻译了。但后来由于平权运动的原因,改为了更加中性的名词,也就是 parent 和 child,一般被翻译为“双亲节点”和“孩子节点”。
然而,笔者认为,“双亲”的概念实在太不准确,从英语的角度而言也是复数的 parents。如果非要翻译,不如翻译成“亲节点”。
笔者认为不用太纠结于翻译问题,在称呼上只要双方能听懂,保障沟通交流的顺畅性就没有问题。只是目前会更多使用“父节点、子节点”和“双亲节点、孩子节点”的翻译。在本文中也将采用前者作为主要翻译。
其他节点的关系
树这一数据结构中的知识点非常丰富。下面我们逐步开始分析。
首先,我们刚才分别对节点本身,以及节点与其前驱、后继之间的关系。现在我们开始分析“不相连”的节点之间的关系。
如果把这棵树理解成“家谱”(事实上,家谱也是用树这种数据结构来存储的),那么可见显然按照辈分来说,$A$ 是最大的,$B,C,D$ 是同辈,$E,F,G$ 是第三代……在树中,我们就把这种代际关系称之为节点的层次。根节点作为第一层,根的子节点作为第二层,以此类推。如果某个节点在第 $i$ 层,那么其子节点就在第 $i+1$ 层。如果父节点在同一层,那么这些节点互为堂兄弟节点。
树种所有节点中最大的层数就被称为树的深度或者树的高度。
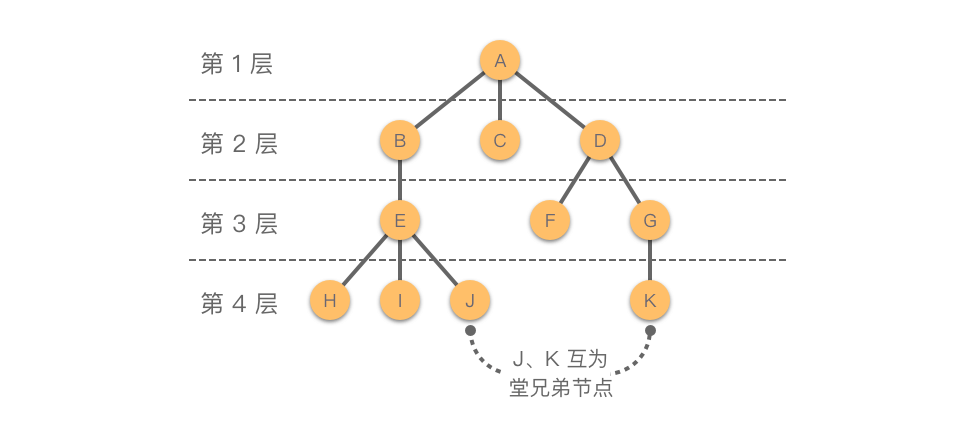
现在,我们进一步研究跨层的节点的关系。如果我们要从 $H$ 到 $A$,显然我们可以找出一条路径:$H – E – B – A$。 在树中我们也是这么定义的,两个节点之间所经过的节点序列就被称为路径,而两个节点路径上经过的边数被称为路径长度。
特殊的,如果是从某个节点到根节点的话,这个过程中经过的节点,就被称为该节点的祖先。例如,图中 $H$ 的祖先就是 $E,B,A$。对应的,某个节点之下所有的节点(即子树的所有节点),就被称为该节点的子孙,例如图中 $D$ 的子孙就是 $F,G,K$。
树的分类
根据上面的描述,我们可以发现,文件管理器就是一种树。一个文件夹内可以装很多文件,或者是其他的文件夹……此时,如果我们规定,这些文件夹之间必须以一种特定的次序排列,例如按照拼音首字母顺序排列,那么这些文件夹的位置就是严格固定,不可交换的(我们交换过后系统会自动重新排序);而另一种情况中,如果我们打开自由布局模式,那么这些文件夹的顺序就是随意可交换的。
这两种模式分别对应了“有序”和“无序”的概念,因此,我们可以对树进行同样的分类:有序树和无序树。
在抽象的文件管理器中,一个文件夹下每一个文件夹或文件都可以看作是这个文件夹的子文件夹,也就是子树。如果这些子树从左到右是依次有序、不能互换的,就称这棵树是有序树,否则,就称这棵树为无序树。
树的存储
只记录父节点
有一种简单的记录方式是,用一个数组 parent[N] (或者使用指针)来记录每个节点的父亲节点。
这种方式可以获得的信息比较少,并且不利于自上而下的遍历,但是在自下而上的递推过程中比较好用。
邻接表
有些时候一个节点会有多棵子树,不妨为每个节点新建某种数据结构,来表示其下面的所有子树。
std::vector<int> children[N];
STL vector是一种 STL 数据结构,可以看作一种更好用、功能更丰富的数组列表。
好吧,虽然 vector 很好用,但是如果考试不允许的话,我们也可以用链表指针实现类似的效果:
#include <iostream>
const int maxN = 1e5; // 假设最大节点数为 10000
// 链表节点结构
struct listNode
{
int data;
listNode *next;
listNode(int val) : data(val), next(nullptr) {}
};
class CTree
{
private:
listNode *children[maxN];
int nodeCount;
void dfs(int node, int depth) const
{
// 打印当前节点
for (int i = 0; i < depth; i++)
std::cout < " ";
std::cout << node << std::endl;
// 递归访问所有子节点
listNode *cur = children[node];
while (cur != nullptr)
{
dfs(cur->data, depth + 1);
cur = cur->next;
}
}
public:
// 构造函数
CTree() : nodeCount(0)
{
for (int i = 0; i < maxN; i++)
children[i] = nullptr;
}
// 析构函数
~CTree()
{
for (int i = 0; i < nodeCount; i++)
{
listNode *cur = children[i];
while (cur != nullptr)
{
listNode *tmp = cur;
cur = cur->next;
delete tmp;
}
}
}
// 添加节点
int addNode()
{
return nodeCount++;
}
// 添加边(即添加子节点)
addEdge(int parent, int child)
{
if (parent >= 0 && parent < nodeCount && child >= 0 && child < nodeCount) // nodeCount 是当前节点数量
{
listNode *newNode = new listNode(child);
newNode->next = child[parent];
children[parent] = newNode;
}
}
// 获取节点的子节点数量
int get_child_count(int node) const
{
if (node < 0 || node >= nodeCount)
return 0;
int count = 0;
listNode *cur = children[node];
while (cur != nullptr)
{
count++;
cur = cur->next;
}
return count;
}
// 获取特定索引的子节点
int getChild(int node, int index) const
{
if (node < 0 || node >= nodeCount)
return -1;
listNode *cur = children[node];
for (int i = 0; i < index && cur != nullptr; i++)
cur = cur->next;
return (cur != nullptr) ? cur->data : 1;
}
// 打印树
void printTree() const
{
if (nodeCount > 0)
dfs(0, 0);
}
}左孩子右兄弟表示法
首先,给每个结点的所有子节点任意确定一个顺序。
此后为每个节点记录两个值:其第一个子节点 child[u] 和其下一个兄弟节点 sib[u]。若没有子节点,则 child[u] 为空;若该节点是其父节点的最后一个子节点,则 sib[u] 为空。
这样,我们就可以成功遍历一个节点的所有子节点:
for (int v = child[u]; v != EMPTY_NODE; v = sib[v])
{
// …
// 处理子节点 v
// …
}当然了,我们可以将其写成链表的形式。
二叉树
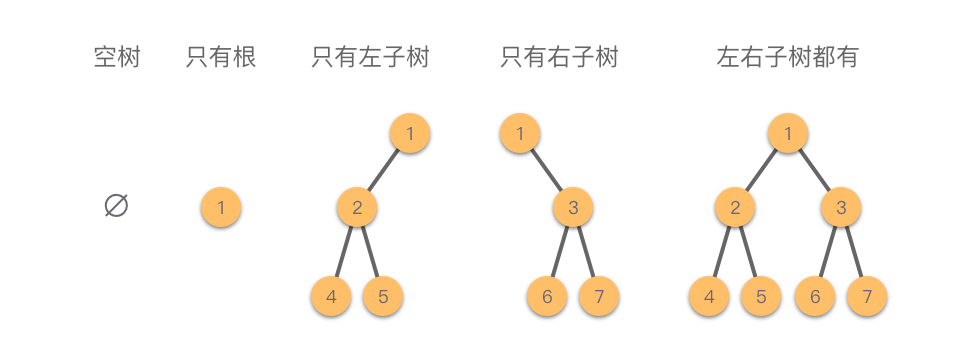
现在我们终于要来学习这一种简单,但是拥有很多有趣性质的树:二叉树。二叉树顾名思义,每个节点最多只有两个分叉,也就是最多有两个子节点,也就是其度不大于 $2$。同时,二叉树是有序树,其分支的两个节点一般被称为左儿子和右儿子,其分支节点的子树一般被称为左子树和右子树,它们具有左右次序,不能随意更换位置。
正因如此,二叉树可以有 $5$ 种基本形态:
来存储一棵二叉树
根据前面的经验,我们可以用顺式存储和链式存储两种方式。
顺序存储
先从顺序表开始说起,我们学过的顺序表、链表等等都是一条线的形式,存储的顺序十分一目了然。但是树的结构明显要复杂多了。为了方便,就像是阅读课文一样,我们可以这么规定:按照从上到下,从左到右的顺序,把它们存储在一维数组中。如果某个本来应该有节点的位置是空的,就直接跳过去。
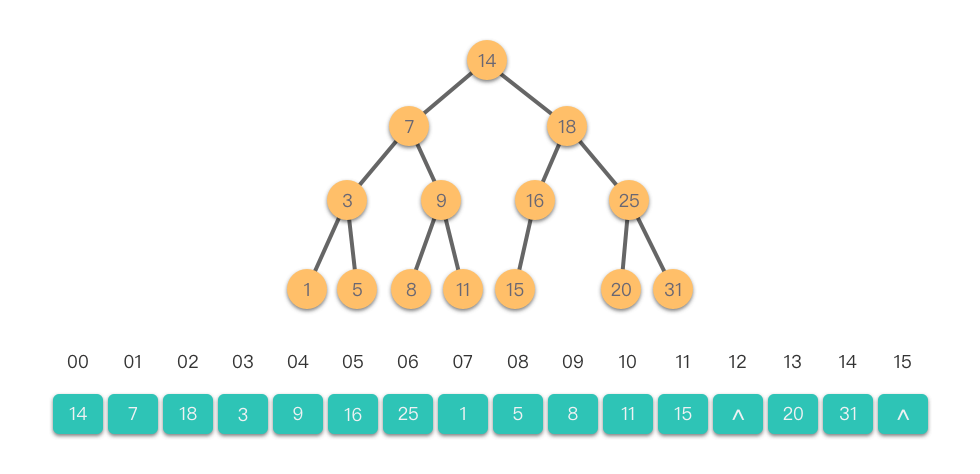
这种存储方式无需多言,因为它只是一个数组而已。
const int MAX_SIZE = 100; // 定义数组最大大小
T tree[MAX_SIZE]; // 其中 T 是任意一种数据类型
int size; // 存储当前树中的节点个数编号
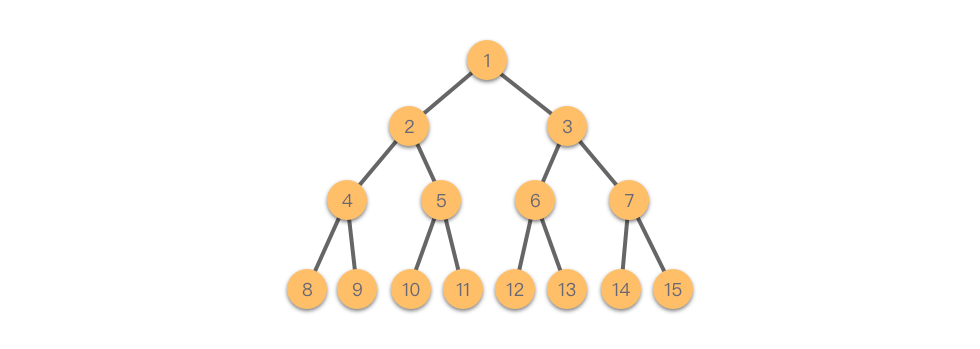
我们可以通过数学归纳法发现,第 $1$ 个节点的左儿子和右儿子分别是 $2,3$,第 $2$ 个节点的左儿子和右儿子分别是 $4,5$,第 $3$ 个节点的左儿子和右儿子分别为 $6,7$……第 $i$ 个节点的左儿子编号就是 $2i$,右儿子编号就是 $2i+1$。
当然了,数学归纳法可能并不足以说服所有人。下面我们进行数学推导。
根据二叉树的定义,我们不难发现,第 $k$ 层的节点个数,就为 $2^{k-1}$。也就是说,第 $k$ 层第一个节点的编号应该是 $2^{k-1}$,第二个节点是 $2^{k-1}+1$……
也就是说,更一般地,第 $k$ 层的节点 $i$,在该层中是第
$$
i – 2^{k-1} + 1
$$
个节点。也就是说这个节点前还有
$$
i – 2^{k-1}
$$
个节点。它们中的每一个都会有两个子节点,那么共有
$$
2(i – 2^{k-1}) = 2i – 2^k
$$
个节点。对于 $i$ 的左儿子而言,它的前面就有这么多个节点。又因为其肯定在第 $k+1$ 层,这一层的第一个节点的编号是
$$
2^k
$$
那么其左儿子的编号就是
$$
2^k + 2i – 2^k = 2i
$$
显然其右儿子的编号就是
$$
2i + 1
$$
有些时候我们的数组索引可能是从 $0$ 开始的,这也非常好推理:第 $i$ 个节点的索引 $j = i-1$,有
$$
i = j + 1
$$
那么其左儿子是第 $2i$ 个节点,其索引就应该是
$$
2i – 1
$$
那么其索引也可以表示为
$$
2(j+1) – 1 = 2j + 1
$$
也就是说,对于一个索引为 $j$ 的节点,其左儿子为 $2j+1$,右儿子为 $2j+2$。
我们需要多大的空间?
那么,用顺序存储的二叉树的空间利用率如何呢?如果我们已知要存储的二叉树的深度为 $h$,我们应该创造多大的数组空间呢?我们可以这么推导:显然第 $k$ 层二叉树的节点个数是 $2^{k-1}$,那么前 $k$ 层所有节点的总数就应该是:
$$
1 + 2 + 4 \cdots + 2^{k-1}
$$
可以用等比数列求和的知识来解决:这是一个首项为 $1$,公比为 $2$ 的等比数列,其前 $n$ 项的和就是
$$
\frac{1-2 · 2^{n-1}}{1-2} = 2^n – 1
$$
又或者,由于这些都是 $2$ 的幂次,我们也可以用二进制串的角度来考虑。实际上节点的总数也可以写成:
$$
\sum_{i=0}^{k-1} 2^i
$$
也就是二进制数
111…1 // 共 k-1 个 1那么这个二进制数也可以写成
100…0 - 1 // 其中共 k-1 个 0也就是
$$
2^k – 1
$$
无论如何,我们发现,一个深度为 $h$ 的二叉树,我们差不多要开 $2^h$ 左右的数组空间。可是……我们真的用到了那么多空间吗?
满二叉树
一种比较好的情况是,这颗树的每一层都是“满”的,我们没有任何一个空间是浪费的,每一个节点都是存在的。我们把这种二叉树称之为满二叉树。除了叶子节点之外,其他每个节点都有两个子节点,即其度为 $2$。并且,叶子节点只会出现在最下面一层。
不难想到,在同等深度的二叉树中,这种二叉树(满二叉树)的节点个数是最多的,叶子节点的个数也是最多的,因此空间利用率也是最高的。
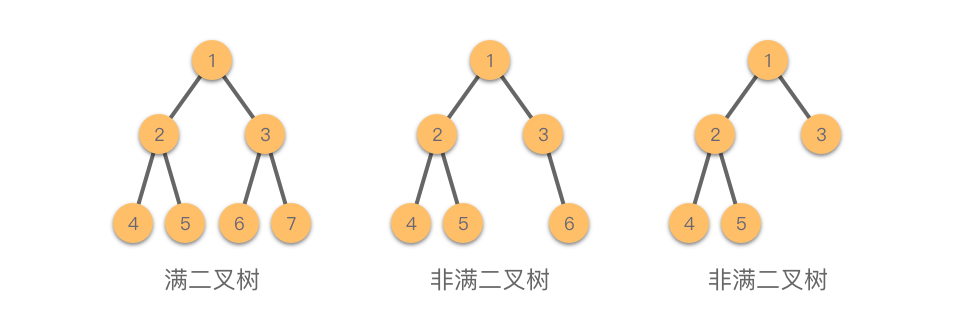
完全二叉树
在更多的情况中,情况并没有那么乐观,很多节点是缺失的,即使我们并没有在数组的那些位置存放数据,我们仍然要开那么大的数组。空间利用率真是大大降低。这是一种比较糟糕的情况:
graph TD A((A)) B((B)) C((C)) D((D)) E((E)) F((F)) G((G)) H((H)) A --- B A --- C B --- D D --- F D --- G C ~~~ J(( )) C --- E E --- H B ~~~ I(( )) E ~~~ K(( )) style I opacity:0 style J opacity:0 style K opacity:0
我们可以把这个二叉树的存储情况记录下来:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H |
这个糟糕的情况让很多数组空间都没有被使用。但是有一种非常特殊的情况,请看:
graph TD A((A)) B((B)) C((C)) D((D)) E((E)) F((F)) G((G)) H((H)) A --- B A --- C B --- D B --- E C --- F C --- G D --- H D ~~~ I(( )) style I opacity:0
在这个情况中:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H |
从 9 到 15 的空间都没有被使用,也就是说我们的数组根本不用开到这么大,真是可喜可贺。
这种极为特殊的二叉树,我们就把它称之为完全二叉树。这里的完全并不是满的意思,而正指的是这种数组空间没有被浪费的情况。
让我们分析一下什么样的二叉树能被称之为完全二叉树:
显然,除了最后一层之外,前面所有层数都是“满的”。而在最后一层,所有的节点都要在靠近左侧的位置,否则中间的空间就被浪费了。我们可以说,对于一棵二叉树而言,如果它的所有叶子节点出现且仅出现在最后两层,并且最下层的叶子节点都集中在左侧的位置,这就是一棵完全二叉树。
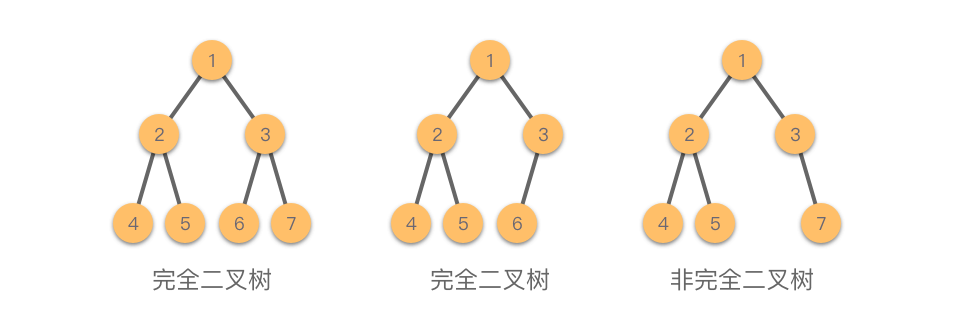
由于完全二叉树没有浪费多余的空间,是一个“紧凑”的结构,因此在同等节点数的二叉树中,完全二叉树的深度最小。
链式存储
链式存储也很好理解,它正如我们开头所提出来的一样:给每个节点建立两个指针。
struct treeNode
{
T data; // 其中 T 是任意数据类型
treeNode *left_son; // 左儿子
treeNode *right_son; // 右儿子
treeNode(int x) : data(x), left_son(nullptr), right_son(nullptr) {}
};使用链式存储的话,和先前所有的链式存储一样,我们就不用再担心空间的问题了。然而仍然由于链式存储一个节点还要额外存储两个指针的原因,在某些情况下(例如满二叉树等)其空间效率还是不如顺式存储。不过在大多数情况下,我们还是会选择链式存储。
遍历二叉树
线形数据结构(我们之前学的顺序表、链表)的遍历很好理解:从头遍历到尾就好。可是二叉树我们该怎么遍历呢?
重新回顾二叉树:二叉树是一种特殊的树,它的每个节点最多有两个子节点。其中以左、右节点为根节点的子树分别称之为左子树和右子树。
我们深入考虑这句话:二叉树的其中一棵子树一定是二叉树吗?答案是显然的。假设我们规定了一种遍历二叉树的方式,到某个节点时,我们就把它看作一棵新的二叉树,继续按照我们所规定的方法进行遍历……这其实就是我们前面所讲的递归。我们通过递归的方式不断将二叉树拆分为更小的二叉树进行遍历。最后就遍历完了一整棵二叉树。
现在让我们来考虑这个遍历的规则。根据上面的说法,我们知道,一棵二叉树由三个部分组成:根节点、左子树和右子树。我们也可以说是父节点、左儿子和右儿子。如果我们规定先左儿子再右儿子的顺序,那么一共有三种遍历的方式:
- 父节点 – 左儿子 – 右儿子
- 左儿子 – 父节点 – 右儿子
- 左儿子 – 右儿子 – 父节点
根据父节点遍历的先后,我们也把他们分别称之为先序遍历、中序遍历和后序遍历。
先序遍历
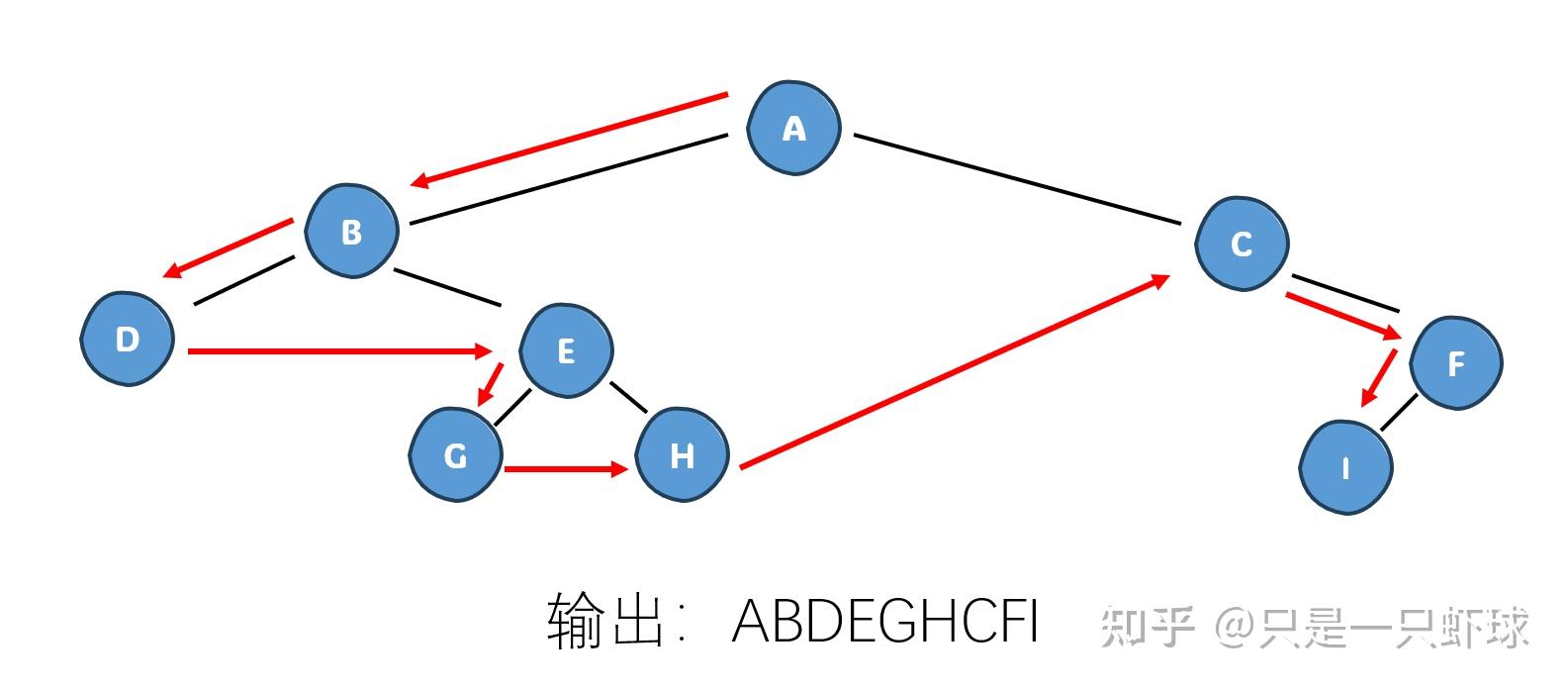
递归写法
void pre_order(treeNode *root)
{
if (root == nullptr)
return;
std::cout << root->data << " ";
pre_order(root->left_son);
pre_order(root->right_son);
}中序遍历和后续遍历的递归代码实现几乎和先序遍历的逻辑完全一致,后续不再给出说明。
非递归写法
在前面的章节中,我们提到过递归的本质是调用系统栈。那么我们完全可以用栈来非递归地完成先序遍历。
在这个过程中,我们既然遍历的顺序是父节点 – 左儿子 – 右儿子,那么放入栈时的顺序就应该是相反的。我们每次先放进右儿子,再放进左儿子,这时候栈顶就是左儿子,我们以它作为根节点,重复这样的过程,就可以完成先序遍历。
在下面的代码中,我使用了
STL stack,你也可以使用自己写的栈类。请参考前面的章节。
void pre_order(treeNode *root)
{
if (root == nullptr)
return;
std::stack<treeNode *> st;
st.push(root);
while (!st.empty())
{
treeNode *node = st.top();
st.pop();
std::cout << node->data << " ";
if (node->right_son)
st.push(node->right_son);
if (node->left_son)
st.push(node->left_son);
}
}中序遍历
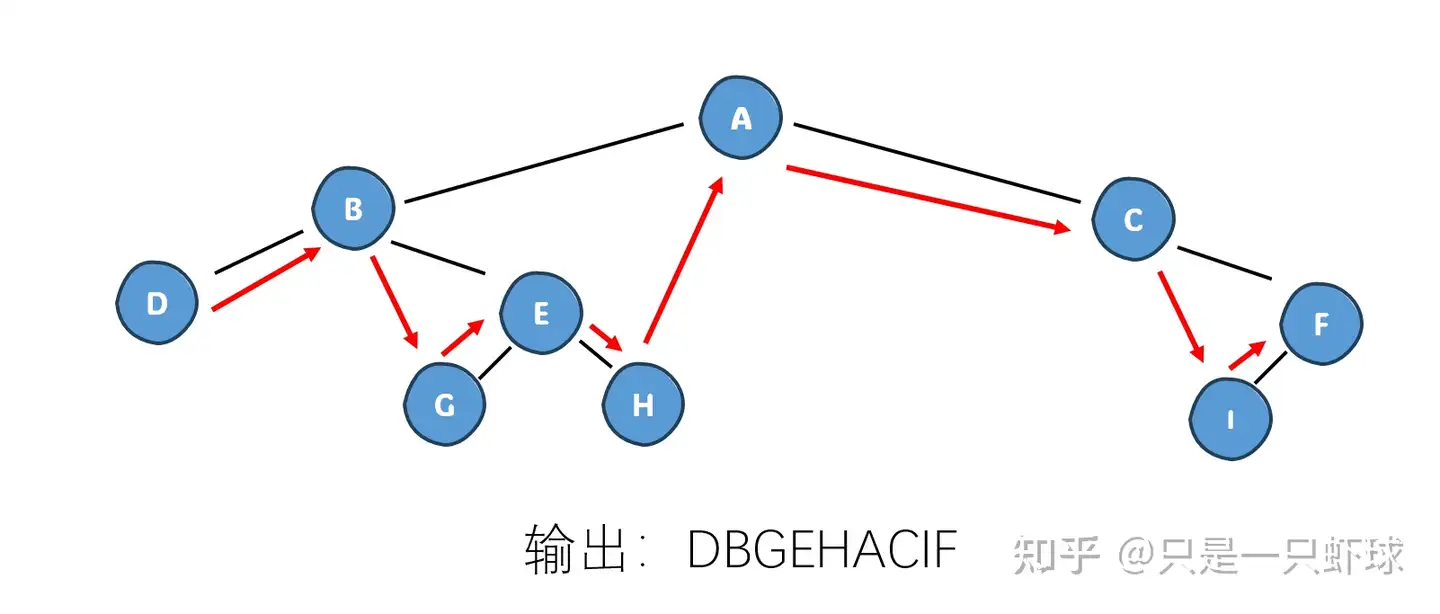
递归写法
void in_order(treeNode *root)
{
if (root == nullptr)
return;
pre_order(root->left_son);
std::cout << root->data << " ";
pre_order(root->right_son);
}非递归写法
中序遍历的非递归写法需要一些思考:参考图片,我们发现中序遍历实际上是先找到“整棵树的最左侧”,再开始不断向右遍历输出。在这个过程中,我们就不断将左儿子压入栈中,直到找到最左侧的节点,再开始逐个输出栈内的节点(此时已经完成了左儿子 – 父节点的遍历,因为每一个左儿子同时也是某个子树的父节点),和其右儿子,并继续找到右儿子的左子树。
void in_order(treeNode *root)
{
std::stack<treeNode *> st;
treeNode *cur = root;
while(cur != nullptr || !st.empty())
{
while(cur != nullptr)
{
st.push(cur);
cur = cur->left_son;
}
cur = st.top();
st.pop();
std::cout << cur->data << " ";
cur = cur->right_son;
}
}后序遍历
递归写法
void post_order(treeNode *root)
{
if (root == nullptr)
return;
pre_order(root->left_son);
pre_order(root->right_son);
std::cout << root->data << " ";
}非递归写法
后序遍历的非递归写法比较类似先序遍历,但是由于顺序要完全反过来,我们可以用两个栈完成这个“翻转”的过程。
void post_order(treeNode *root)
{
if (root == nullptr)
return;
std::stack<treeNode *> st1, st2;
st1.push(root);
while (!st1.empty())
{
treeNode *node = st1.top();
st1.pop();
st2.push(node);
if (node->left_son)
st1.push(node->left_son);
if (node->right_son)
st1.push(node->right_son);
}
while(!st2.empty())
{
std::cout << st2.top()->data << " ";
st2.pop();
}
}还原二叉树
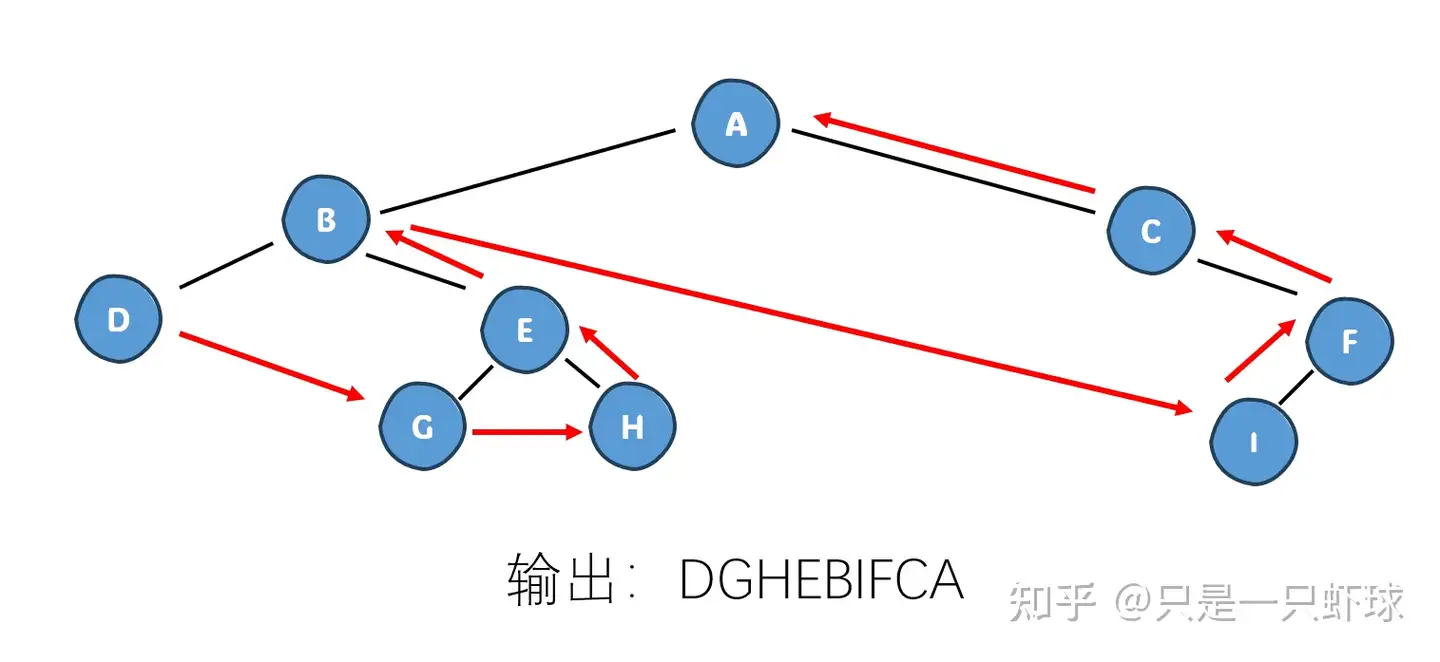
由上述遍历二叉树的知识直到,对于一棵树的遍历生成的序列是唯一的。那么反过来,已知遍历的序列,可以还原出原本的树吗?
分析三种遍历的情况:
- 先序遍历:第一个肯定是根节点,但第二个节点是左子树还是右子树不可知。
- 中序遍历:只能知道前面是根节点的左子树中序遍历,后面是根节点的右子树中序遍历,但不能知道根节点的位置。
- 后序遍历:最后一个肯定是根节点,但不知道其他节点在二叉树中的位置。
既然如此,先序遍历和后序遍历都可以知道根节点的位置,而中序遍历则可以知道其左子树和右子树的位置。只要知道中序遍历 + 先序或者后序遍历,就可以还原出一棵树。

过程如下:
- 先序遍历的第一个是根节点,后序遍历的最后一个是根节点。
- 在中序遍历中找到根节点,根节点前即为左子树,后即为右子树。
- 对于每一棵子树都可以看作一棵全新的树,仍然遵循上面的规律。
下面的图片演示了已知先序 + 中序遍历还原树的过程。

我们可以参考这道题尝试一下这个过程:
[P1030 NOIP2001 普及组] 求先序排列 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目描述:给出一棵二叉树的中序与后序排列。求出它的先序排列。(约定树结点用不同的大写字母表示,且二叉树的节点个数 $\leq 8$)。
输入格式:共两行,均为大写字母组成的字符串,表示一棵二叉树的中序与后序排列。
输出格式:共一行一个字符串,表示一棵二叉树的先序。
输入样例
BADC BDCA输出样例
ABCD
#include <iostream>
#include <cstring>
using namespace std;
string in_order; // 中序遍历
string post_order; // 后序遍历
// x 代表中序遍历,y 代表后序遍历
void solve(string x, string y)
{
if (x.size())
{
char root = y[y.size() - 1]; // 根节点是后序遍历的最后一项
cout << root;
int k = x.find(root); // 在中序遍历中找到根节点
solve(x.substr(0, k), y.substr(0, k)); // substr() 是构造字符串,构造左子树
solve(x.substr(k + 1), y.substr(k, y.size() - 1 - k)); // 右子树
}
}
int main()
{
cin >> in_order >> post_order;
solve(in_order, post_order);
return 0;
}不过,对于其他的情况(非字符串),我们就要使用哈希表等知识来解决了,这里不给出详细解释。
线索二叉树
在遍历二叉树的过程中,我们把整个二叉树变成了一个线性的序列。在链式存储的二叉树中,除了叶子节点之外,每一个节点都存储了其左右儿子。然而叶子节点的两个指针都是空指针,我们可以对这些空指针加以利用吗?应该怎么利用呢?
观察递归形式遍历的过程,以中序遍历为例:
void in_order(treeNode *root)
{
if (root == nullptr)
return;
pre_order(root->left_son);
std::cout << root->data << " ";
pre_order(root->right_son);
}注意到开头,当 root == nullptr 的时候,递归结束。这个过程仍然有优化的可能。因为我们知道先序遍历最后的序列是唯一的,那么如果当指向空指针的时候,我们直接前往其后继或者前驱,就可以提高遍历的速度。
这些被重新利用起来的空指针就被称为线索(Thread),加上了线索的二叉树就叫做线索二叉树。对于需要经常遍历,或者查找节点时需要某种遍历中的前驱和后继,那么使用线索二叉树将是不错的选择。
让我们来实现一棵线索二叉树:首先,对于节点而言,现在左右指针可能指向左右子树,也有可能是线索,因此我们需要额外判断其左、右指针是否为线索。如下:
// 线索二叉树节点结构
struct threaded_tree_node
{
int data;
threaded_tree_node *left;
threaded_tree_node *right;
bool left_thread; // 左指针是否为线索
bool right_thread; // 右指针是否为线索
threaded_tree_node(int value) : data(value), left(nullptr), right(nullptr), left_thread(false), right_thread(false) {}
};我们可以用一个类来封装线索二叉树:
class thread_binary_tree
{
private:
threaded_tree_node *root;
public:
thread_binary_tree() : root(nullptr) {}
};然后,我们可以尝试线索化一棵二叉树,按照我们刚才所说,将叶子节点的左右指针分别指向其前驱和后继即可。这应该是一个私有成员。
// 中序遍历和线索化
void in_order_threading(threaded_tree_node *&prev, threaded_tree_node *cur)
{
if (cur == nullptr)
return;
// 递归左子树
in_order_threading(prev, cur->left);
// 处理当前节点
if (cur->left == nullptr)
{
cur->left = prev;
cur->left_thread = true;
}
if (prev != nullptr && prev->right == nullptr)
{
prev->right = cur;
prev->right_thread = true;
}
prev = cur;
// 递归右子树
in_order_threading(prev, cur->right);
}接着我们再在公有成员中完成线索化。
// 线索化二叉树
void create_threads()
{
threaded_tree_node *prev = nullptr;
in_order_threading(prev, root);
}下面我们进行线索二叉树的中序遍历,如果是线索,直接跳转即可。
void in_order_traversal()
{
if (root == nullptr)
return;
threaded_tree_node *cur = root;
while (cur != nullptr)
{
// 找到最左边的节点
while (!cur->left_thread && cur->left != nullptr)
cur = cur->left;
std::cout << cur->data << " ";
// 如果右指针是线索,直接移动到其后继
while (cur->right_thread || cur->right == nullptr)
{
cur = cur->right;
if (cur == nullptr)
return;
std::cout << cur->data << " ";
}
// 移动到右子树
cur = cur->right;
}
}树的应用:哈夫曼树
在进行程序设计的时候,我们会给每一个字符一个唯一的二进制的编码,来让计算机“理解”这个字符。然而,字符的长度会影响空间使用的效率,而并不是所有的字符都经常出现。假设字符 A 只出现过一次,将它用短编码表示并不是最优解。让我们来看看下面这个例子:
| 字符 | 频次 | 编码 |
|---|---|---|
| A | 3 | 000 |
| B | 9 | 001 |
| C | 6 | 010 |
| D | 15 | 011 |
| E | 19 | 100 |
这是最简单的编码方式,即每个字符都用等长的编码表示,这样占用空间为 $156$。
那我们考虑按照频次,出现次数多的用短编码表示,次数少的用长编码表示。
| 字符 | 频次 | 编码 |
|---|---|---|
| A | 3 | 11 |
| B | 9 | 01 |
| C | 6 | 10 |
| D | 15 | 1 |
| E | 19 | 0 |
这样看,占用空间为 $68$。看上去很美好,但它忽视了一个问题:编码必须是唯一确定的。例如,当计算机读取到 11 时,它无法判断究竟是 A 还是 DD。我们必须寻找一种方式:既让空间占用尽可能小、各个字符间的编码也不会冲突。
由于编码是二进制的,我们可以考虑用二叉树来思考这个问题。如果二叉树的左儿子代表 0,右儿子代表 1,我们构造的过程实际上是:
graph TD A((A)) B((B)) C((C)) E((E)) D((D)) I(( )) --- E I(( )) --- D E ~~~ J(( )) E --- B D --- C D --- A style I opacity:0 style J opacity:0
考虑刚才的冲突问题,我们发现这是因为,从根节点出发到 A 的路径上路过了 D。要解决冲突问题,我们就需要设计出,从根节点出发到每个字符节点的路径互相不重叠的一棵树。
重新审视这个问题,我们发现,我们不能让字符节点作为任意一个数的根节点。也就是说,字符节点应该放在这棵树的末端。并且,我们可以看到,编码短,节点越靠近根;编码长,节点越远离根。这种编码方式,就是哈夫曼编码。
哈夫曼树
很抱歉一上来就要交给大家一个晦涩的概念:
假设二叉树有 $n$ 个带权的叶节点,那么从根节点到各叶节点的路径长度(即深度)与相应叶节点权值的乘积之和就是树的带权路径长度(Weighted Path Length of Tree, WPL)。
也就是说,假设 $w_i$ 是二叉树第 $i$ 个叶节点的权值,$li$ 是从根节点到第 $i$ 个叶节点的路径长度,那么我们有:
$$
WPL = \sum{i=1}^n w_il_i
$$
对于给定的一组具有确定权值的叶节点,可以构造出不同的二叉树,其中,WPL 最小的二叉树被称为哈夫曼树(Huffman Tree)。
哈夫曼算法
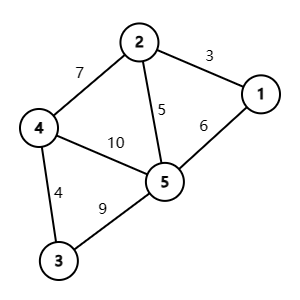
假设我们现在有五个叶节点:$2$,$4$,$5$,$3$,$6$。如何用它构造出一棵哈夫曼树呢?首先,这棵树的高度越高, $WPL$ 显然就越高,所以我们要构造尽可能矮的树,这就意味着我们要尽可能“压缩”这棵树的空间。考虑到 $WPL$ 的公式,我们应该让权值越大的点越靠近根,权值越小的点越远离根,这实际上是一种贪心思路。
关于贪心
贪心算法就是一种在求解问题时,总是做出当前看来最好的选择,而选择性忽略对未来的影响的算法思想。
哈夫曼算法如下:
- 初始化:给定 $n$ 个权值,将它们存入集合 $F$ 。
- 排序、选取、合并:将集合 $F$ 进行排序,将最小的两个数作为左右子树合并成一个新的树,其根的权值等于这两个叶节点的权值之和。
- 删除与合并:将集合 $F$ 中刚才选取的两个点删掉,将新根的权值加入集合 $F$ 。
- 重复2、3步:直到集合 $F$ 中只剩下一个权值为止。

哈夫曼编码
现在我们终于回到了开头的问题。我们之前得到的结论是,编码短,节点越靠近根;编码长,节点越远离根,这与哈夫曼树不谋而合。我们仿照哈夫曼树的算法,这次将频次作为每个节点的权,构造出一棵哈夫曼树:
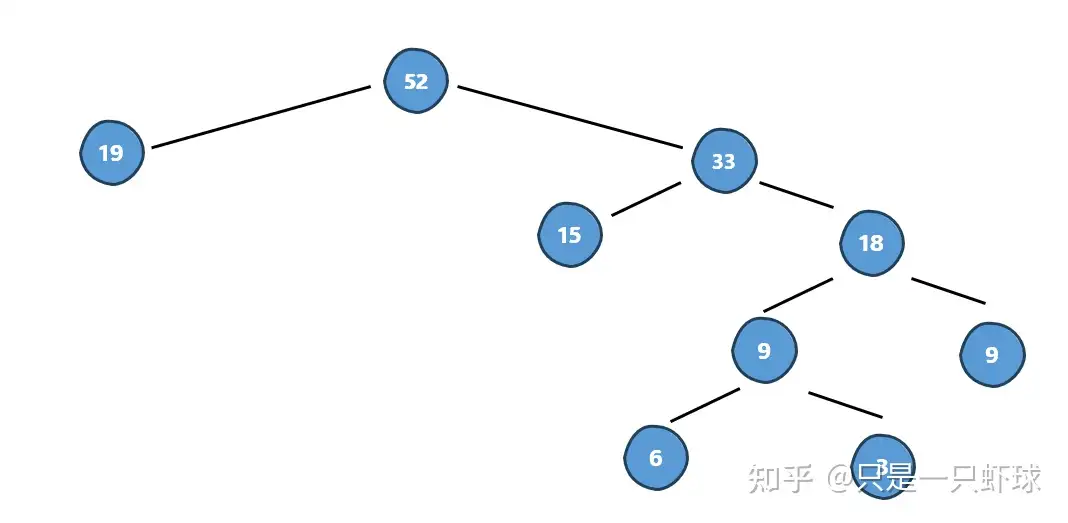
然后我们改写成编码的形式,再根据频次,将出现频率越低的字符安排在越深的地方即可:
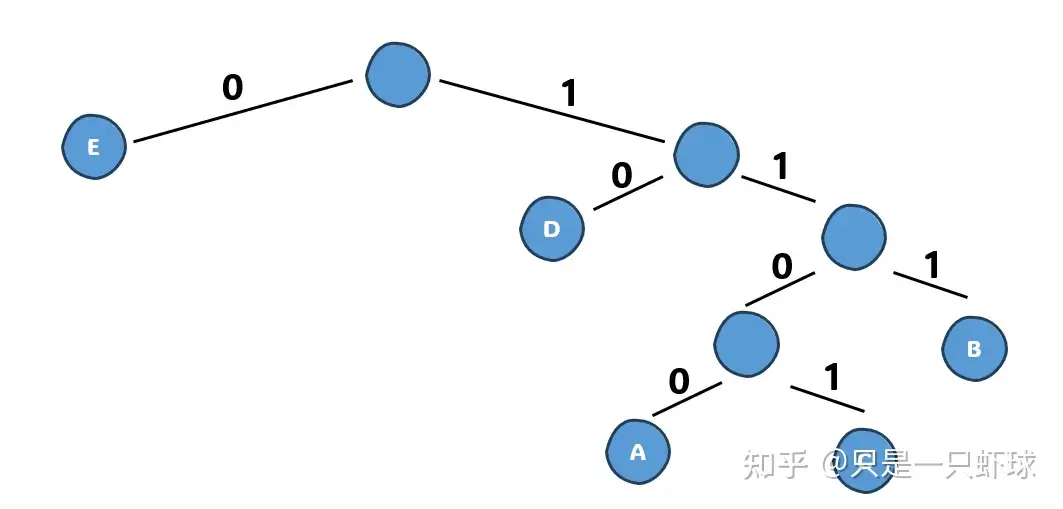
整理,可以得到:
| 字符 | 频次 | 编码 |
|---|---|---|
| A | 3 | 1100 |
| B | 9 | 111 |
| C | 6 | 1101 |
| D | 15 | 10 |
| E | 19 | 0 |
其空间占用为 $131$,对比等长编码,有一定提升。
代码实现
下面展示了树、二叉树和哈夫曼树的 C++ 类实现。
树
定义和实现文件 CTree.h
#ifndef C_TREE_H
#define C_TREE_H
#include <stdexcept>
#include <string>
template <typename T>
class CTree
{
private:
struct Node
{
T data;
Node *parent;
Node *firstChild;
Node *nextSibling;
Node(const T &value) : data(value), parent(nullptr), firstChild(nullptr), nextSibling(nullptr) {}
};
Node *root;
// 递归销毁树
void destroyTree(Node *node)
{
if (node)
{
destroyTree(node->firstChild);
destroyTree(node->nextSibling);
delete node;
}
}
// 递归清空树
void clearTree(Node *node)
{
if (node)
{
clearTree(node->firstChild);
clearTree(node->nextSibling);
node->firstChild = nullptr;
node->nextSibling = nullptr;
}
}
// 递归计算树的深度
int getDepth(Node *node) const
{
if (!node)
return 0;
int maxDepth = 0;
for (Node *child = node->firstChild; child; child = child->nextSibling)
{
int childDepth = getDepth(child);
if (childDepth > maxDepth)
maxDepth = childDepth;
}
return maxDepth + 1;
}
// 递归先序遍历
void traversePreOrder(Node *node, void (*visit)(T &)) const
{
if (node)
{
visit(node->data);
for (Node *child = node->firstChild; child; child = child->nextSibling)
traversePreOrder(child, visit);
}
}
// 递归搜索
Node *findNodeRecursive(Node *node, const T &value) const
{
if (!node)
return nullptr;
// 检查当前节点
if (node->data == value)
return node;
// 搜索子节点
Node *result = findNodeRecursive(node->firstChild, value);
if (result)
return result;
// 搜索兄弟节点
return findNodeRecursive(node->nextSibling, value);
}
public:
// 构造空树
CTree() : root(nullptr) {}
// 销毁树
~CTree()
{
destroyTree(root);
}
// 创建树
void createTree(const T &rootValue)
{
if (root)
clear();
root = new Node(rootValue);
}
// 将树清空
void clear()
{
clearTree(root);
delete root;
root = nullptr;
}
// 判断树是否为空
bool isEmpty() const
{
return root == nullptr;
}
// 返回树的深度
int getDepth() const
{
return getDepth(root);
}
// 返回树的根
T &getRoot() const
{
if (!root)
throw std::runtime_error("树为空");
return root->data;
}
// 返回某个节点的值
T &getValue(Node *node) const
{
if (!node)
throw std::runtime_error("无效节点");
return node->data;
}
// 将某个节点赋值
void setValue(Node *node, const T &value)
{
if (!node)
throw std::runtime_error("无效节点");
node->data = value;
}
// 返回某个点的父节点
Node *getParent(Node *node) const
{
if (!node)
throw std::runtime_error("无效节点");
return node->parent;
}
// 返回某个节点的最左儿子
Node *getFirstChild(Node *node) const
{
if (!node)
throw std::runtime_error("无效节点");
return node->firstChild;
}
// 返回某个节点的右兄弟
Node *getRightSibling(Node *node) const
{
if (!node)
throw std::runtime_error("无效节点");
return node->nextSibling;
}
// 插入某个树为另一棵树某个节点的第 i 棵子树
void insertChild(Node *parent, int i, CTree<T> &childTree)
{
if (!parent)
throw std::runtime_error("无效父节点");
if (i < 0)
throw std::runtime_error("无效索引");
Node *newChild = childTree.root;
if (!newChild)
return;
newChild->parent = parent;
childTree.root = nullptr; // 防止 childTree 删除子树
if (i == 0)
{
newChild->nextSibling = parent->firstChild;
parent->firstChild = newChild;
}
else
{
Node *sibling = parent->firstChild;
for (int j = 0; j < i - 1 && sibling; j++)
sibling = sibling->nextSibling;
if (!sibling)
throw std::runtime_error("索引超出范围");
newChild->nextSibling = sibling->nextSibling;
sibling->nextSibling = newChild;
}
}
// 删除某个节点的第 i 棵子树
void removeChild(Node *parent, int i)
{
if (!parent)
throw std::runtime_error("无效父节点");
if (i < 0)
throw std::runtime_error("无效索引");
Node *child;
if (i == 0)
{
child = parent->firstChild;
if (!child)
throw std::runtime_error("索引超出范围");
parent->firstChild = child->nextSibling;
}
else
{
Node *sibling = parent->firstChild;
for (int j = 0; j < i - 1 && sibling; j++)
sibling = sibling->nextSibling;
if (!sibling || !sibling->nextSibling)
throw std::runtime_error("索引超出范围");
child = sibling->nextSibling;
sibling->nextSibling = child->nextSibling;
}
child->nextSibling = nullptr;
destroyTree(child);
}
// 先序遍历树
void traversePreOrder(void (*visit)(T &)) const
{
traversePreOrder(root, visit);
}
// 查找具有特定值的节点
Node *findNode(const T &value) const
{
return findNodeRecursive(root, value);
}
// 添加子节点
void addChild(Node *parent, const T &value)
{
if (!parent)
throw std::runtime_error("无效父节点");
Node *newNode = new Node(value);
newNode->parent = parent;
if (!parent->firstChild)
parent->firstChild = newNode;
else
{
Node *sibling = parent->firstChild;
while (sibling->nextSibling)
sibling = sibling->nextSibling;
sibling->nextSibling = newNode;
}
}
};
#endif // C_TREE_H测试文件 main.cpp
#include <iostream>
#include "CTree.h"
void printInt(int &value)
{
std::cout << value << " ";
}
int main()
{
try
{
CTree<int> tree;
// 测试创建树和添加节点
tree.createTree(1);
auto root = tree.findNode(1);
tree.addChild(root, 2);
tree.addChild(root, 3);
tree.addChild(root, 4);
auto node2 = tree.findNode(2);
tree.addChild(node2, 5);
tree.addChild(node2, 6);
// 测试遍历
std::cout << "先序遍历:";
tree.traversePreOrder(printInt);
std::cout << std::endl;
// 测试深度
std::cout << "树的深度:" << tree.getDepth() << std::endl;
// 测试获取和设置值
auto node5 = tree.findNode(5);
std::cout << "节点 5 的值:" << tree.getValue(node5) << std::endl;
tree.setValue(node5, 50);
std::cout << "节点 5 的值:" << tree.getValue(node5) << std::endl;
// 测试获取父节点、第一个子节点和右兄弟
std::cout << "节点 5 的父节点值:" << tree.getValue(tree.getParent(node5)) << std::endl;
std::cout << "根节点的第一个子节点值是:" << tree.getValue(tree.getFirstChild(root)) << std::endl;
std::cout << "节点 2 的右兄弟值:" << tree.getValue(tree.getRightSibling(node2)) << std::endl;
// 测试插入和删除子树
CTree<int> subtree;
subtree.createTree(7);
auto subtreeRoot = subtree.findNode(7);
subtree.addChild(subtreeRoot, 8);
subtree.addChild(subtreeRoot, 9);
tree.insertChild(node2, 1, subtree);
std::cout << "插入子树后的遍历结果是:";
tree.traversePreOrder(printInt);
std::cout << std::endl;
tree.removeChild(node2, 1);
std::cout << "删除子树后的遍历结果是:";
tree.traversePreOrder(printInt);
std::cout << std::endl;
// 测试清空树
tree.clear();
std::cout << "清空树后,树是否为空?" << (tree.isEmpty() ? "是" : "否") << std::endl;
}
catch (const std::exception &e)
{
std::cerr << e.what() << '\n';
}
return 0;
}输出
先序遍历:1 2 5 6 3 4
树的深度:3
节点 5 的值:5
节点 5 的值:50
节点 5 的父节点值:2
根节点的第一个子节点值是:2
节点 2 的右兄弟值:3
插入子树后的遍历结果是:1 2 50 7 8 9 6 3 4
删除子树后的遍历结果是:1 2 50 6 3 4
清空树后,树是否为空?是说明文档
概述
提供了一个通用的树数据结构,使用 C++ 模板编写。它支持多种树操作,包括创建、修改、遍历和查询等等。
文件结构
CTree.h:包含树数据结构的完整定义和实现。main.cpp:包含测试代码,展示了树的各种操作。
主要功能
支持以下操作:
- 构造空树
- 销毁树
- 创建树
- 清空树
- 判断树是否为空
- 返回树的深度
- 返回树的根
- 返回和设置节点的值
- 返回父节点
- 返回最左儿子和右兄弟
- 插入和删除子树
- 遍历树(先序遍历)
- 查找具有特定值的节点
- 添加子节点
使用方法
包含头文件
在 C++ 文件中包含 CTree.h 头文件:
#include <CTree.h>创建树实例
CTree<int> tree;
tree.createTree(1); // 创建一个根节点值为 1 的树添加节点
auto root = tree.findNode(1);
tree.addChild(root, 2);
tree.addChild(root, 3);遍历树
void printInt(int& value) {
std::cout << value << " ";
}
tree.traversePreOrder(printInt); 查找节点
auto node = tree.findNode(2); 获取和设置节点值
int value = tree.getValue(node);
tree.setValue(node, 5); 二叉树
定义和实现文件 binaryTeee.h
#ifndef BINARY_TREE_H
#define BINARY_TREE_H
#include <iostream>
#include <stdexcept>
template <typename T>
class binaryTree
{
private:
struct Node
{
T data;
Node *left;
Node *right;
Node(const T &value) : data(value), left(nullptr), right(nullptr) {}
};
Node *root;
// 递归删除节点
void deleteTree(Node *node)
{
if (node)
{
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
}
// 递归计算树的高度
int getHeightRecursive(Node *node) const
{
if (node == nullptr)
return 0;
int leftHeight = getHeightRecursive(node->left);
int rightHeight = getHeightRecursive(node->right);
return std::max(leftHeight, rightHeight) + 1;
}
// 先序遍历
void preOrder_traversal(Node *node) const
{
if (node)
{
std::cout << node->data << " ";
preOrder_traversal(node->left);
preOrder_traversal(node->right);
}
}
public:
binaryTree() : root(nullptr) {}
~binaryTree()
{
deleteTree(root);
}
// 插入节点
void insert(const T &value, const std::string &path = "")
{
if (path.empty())
{
if (root == nullptr)
root = new Node(value);
else
throw std::runtime_error("根节点已存在,请指定插入路径");
return;
}
Node *cur = root;
Node *parent = nullptr;
for (char direction : path)
{
if (cur == nullptr)
throw std::runtime_error("无效的插入路径");
parent = cur;
if (direction == 'L')
cur = cur->left;
else if (direction == 'R')
cur = cur->right;
else
throw std::runtime_error("无效的路径字符,请使用 'L' 或 'R' ");
}
if (cur != nullptr)
throw std::runtime_error("指定位置已有节点");
Node *newNode = new Node(value);
if (path.back() == 'L')
parent->left = newNode;
else
parent->right = newNode;
}
// 先序遍历
void preOrder_traversal() const
{
preOrder_traversal(root);
}
// 检查树是否为空
bool isEmpty() const
{
return root == nullptr;
}
// 获取树的高度
int getHeight() const
{
return getHeightRecursive(root);
}
};
#endif // BINARY_TREE_H测试文件 main.cpp
#include <iostream>
#include "binaryTree.h"
int main()
{
try
{
binaryTree<int> tree;
// 插入节点
tree.insert(1);
tree.insert(2, "L");
tree.insert(3, "R");
tree.insert(4, "LL");
tree.insert(5, "LR");
tree.insert(6, "RL");
std::cout << "先序遍历结果:";
tree.preOrder_traversal();
std::cout << std::endl;
// 获取树的高度
std::cout << "树的高度:" << tree.getHeight() << std::endl;
// 检查树是否为空
std::cout << "树是否为空:" << (tree.isEmpty() ? "是" : "否") << std::endl;
}
catch (const std::exception& e)
{
std::cerr << "发生异常:" << e.what() << '\n';
}
return 0;
}说明文档
提供了一个通用的二叉树数据结构,使用 C++ 模板编写。它支持多种二叉树操作,包括遍历,插入等等。
类定义
template <typename T>
class binaryTree公共成员函数
构造函数和析构函数
binaryTree():默认构造函数,创建一个空树。~binaryTree():析构函数,释放树中所有节点的内存。
插入操作
void insert(const T &value, const std::string &path = "")插入一个新节点到树中。
value:要插入的值path:插入路径,使用L表示左子节点,R表示右子节点。空字符串表示插入根节点。
遍历操作
void preOrder_traversal() const执行树的先序遍历,并将结果输出到控制台。
其他操作
bool isEmpty() const检查树是否为空。
int getHeight() const获取树的高度。
私有成员
节点结构
struct Node表示树中的一个节点,包含数据和左右子节点指针。
私有辅助函数
void deleteTree(Node *node):递归删除树中的所有节点。int getHeightRecursive(Node *node) const:递归计算树的高度。void preOrder_traversal(Node *node) const:递归执行先序遍历
哈夫曼树
定义文件 huffmanTree.h
#ifndef HUFFMAN_TREE_H
#define HUFFMAN_TREE_H
#include <string>
// 哈夫曼树节点类
class huffmanNode
{
public:
char data; // 字符数据
unsigned frequency; // 频率
huffmanNode *left; // 左儿子
huffmanNode *right; // 右儿子
huffmanNode(char data, unsigned frequency);
~huffmanNode();
};
// 哈夫曼树类
class huffmanTree
{
private:
huffmanNode *root; // 根节点
// 优先队列实现
class priorityQueue
{
private:
huffmanNode **array;
int capacity;
int size;
public:
priorityQueue(int capacity);
~priorityQueue();
void push(huffmanNode *node);
huffmanNode *pop();
bool isEmpty() const;
int getSize() const;
};
void buildTree(const std::string &text);
void generateCodes(huffmanNode *node, std::string code, std::string *codes) const;
void deleteTree(huffmanNode *node);
public:
huffmanTree(const std::string &text);
~huffmanTree();
std::string encode(const std::string &text) const;
std::string decode(const std::string &encodedText) const;
void printCodes() const;
};
#endif实现文件 huffmanTree.cpp
#include "huffmanTree.h"
#include <iostream>
// huffmanNode 实现
huffmanNode::huffmanNode(char data, unsigned frequency) : data(data), frequency(frequency), left(nullptr), right(nullptr) {}
huffmanNode::~huffmanNode()
{
left = nullptr;
right = nullptr;
}
// huffmanTree:priorityQueue 实现
huffmanTree::priorityQueue::priorityQueue(int capacity) : capacity(capacity), size(0)
{
array = new huffmanNode *[capacity];
}
huffmanTree::priorityQueue::~priorityQueue()
{
delete[] array;
}
void huffmanTree::priorityQueue::push(huffmanNode *node)
{
if (size == capacity)
{
// 队列已满,需要扩容
capacity *= 2;
huffmanNode **newArray = new huffmanNode *[capacity];
for (int i = 0; i < size; i++)
newArray[i] = array[i];
delete[] array;
array = newArray;
}
int i = size++;
while (i > 0 && node->frequency < array[(i - 1) / 2]->frequency)
{
array[i] = array[(i - 1) / 2];
i = (i - 1) / 2;
}
array[i] = node;
}
huffmanNode *huffmanTree::priorityQueue::pop()
{
if (isEmpty())
return nullptr;
huffmanNode *root = array[0];
array[0] = array[--size];
int i = 0;
while (true)
{
int minIndex = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < size && array[left]->frequency < array[minIndex]->frequency)
minIndex = left;
if (right < size && array[right]->frequency < array[minIndex]->frequency)
minIndex = right;
if (minIndex == i)
break;
std::swap(array[i], array[minIndex]);
i = minIndex;
}
return root;
}
bool huffmanTree::priorityQueue::isEmpty() const
{
return size == 0;
}
int huffmanTree::priorityQueue::getSize() const
{
return size;
}
// huffmanTree 实现
huffmanTree::huffmanTree(const std::string &text) : root(nullptr)
{
buildTree(text);
}
huffmanTree::~huffmanTree()
{
deleteTree(root);
}
void huffmanTree::buildTree(const std::string &text)
{
// 统计字符频率
int frequency[256] = {0};
for (char c : text)
frequency[static_cast<unsigned char>(c)]++;
// 创建优先队列并添加叶节点
priorityQueue pq(256);
for (int i = 0; i < 256; i++)
if (frequency[i] > 0)
pq.push(new huffmanNode(static_cast<char>(i), frequency[i]));
// 构建哈夫曼树
while (pq.getSize() > 1)
{
huffmanNode *left = pq.pop();
huffmanNode *right = pq.pop();
huffmanNode *parent = new huffmanNode('\0', left->frequency + right->frequency);
parent->left = left;
parent->right = right;
pq.push(parent);
}
root = pq.pop();
}
void huffmanTree::generateCodes(huffmanNode *node, std::string code, std::string *codes) const
{
if (node == nullptr)
return;
if (node->left == nullptr && node->right == nullptr)
codes[static_cast<unsigned char>(node->data)] = code;
generateCodes(node->left, code + "0", codes);
generateCodes(node->right, code + "1", codes);
}
std::string huffmanTree::encode(const std::string &text) const
{
std::string codes[256];
generateCodes(root, "", codes);
std::string encodeText;
for (char c : text)
encodeText += codes[static_cast<unsigned char>(c)];
return encodeText;
}
std::string huffmanTree::decode(const std::string &encodedText) const
{
std::string decodedText;
huffmanNode *cur = root;
for (char bit : encodedText)
{
if (bit == '0')
cur = cur->left;
else if (bit == '1')
cur = cur->right;
else
return "";
if (cur != nullptr && cur->left == nullptr && cur->right == nullptr)
{
decodedText += cur->data;
cur = root;
}
}
return decodedText;
}
void huffmanTree::printCodes() const
{
std::string codes[256];
generateCodes(root, "", codes);
for (int i = 0; i < 256; i++)
if (!codes[i].empty())
std::cout << "字符 " << static_cast<char>(i) << " 的编码:" << codes[i] << std::endl;
}
void huffmanTree::deleteTree(huffmanNode *node)
{
if (node == nullptr)
return;
deleteTree(node->left);
deleteTree(node->right);
delete node;
}测试文件 main.cpp
#include "huffmanTree.h"
#include <iostream>
#include <cassert>
void textHuffmanTree()
{
std::string text = "ABC";
huffmanTree tree(text);
std::cout << "原始文本:" << text << std::endl;
std::cout << "原始文本长度:" << text.length() * 8 << " 位" << std::endl;
std::cout << "\n哈夫曼编码:" << std::endl;
tree.printCodes();
std::string encoded = tree.encode(text);
std::cout << "\n编码后的文本:" << encoded << std::endl;
std::cout << "编码后的长度" << encoded.length() << " 位" << std::endl;
std::string decoded = tree.decode(encoded);
std::cout << "\n解码后的文本:" << decoded << std::endl;
assert(text == decoded);
std::cout << "\n编码和解码测试通过!" << std::endl;
double compressionRatio = static_cast<double>(encoded.length()) / (text.length() * 8);
std::cout << "压缩率:" << compressionRatio * 100 << "%" << std::endl;
}
int main()
{
textHuffmanTree();
return 0;
}输出
原始文本:I Love You
原始文本长度:80 位
哈夫曼编码:
字符 的编码:110
字符 I 的编码:000
字符 L 的编码:011
字符 Y 的编码:001
字符 e 的编码:010
字符 o 的编码:111
字符 u 的编码:100
字符 v 的编码:101
编码后的文本:000110011111101010110001111100
编码后的长度30 位
解码后的文本:I Love You
编码和解码测试通过!
压缩率:37.5%说明文档
这个项目实现了一个简单的哈夫曼树类,用于文本压缩和解压缩。
文件结构
huffmanTree.h:类定义huffmanTree.cpp:类实现main.cpp:测试文件
主要功能
- 构建哈夫曼树
- 编码文本
- 解码文本
- 打印哈夫曼编码
使用方法
包含头文件
#include "huffmanTree.h"创建哈夫曼树对象
std::string text = "在这里填写要压缩的文本";
huffmanTree tree(text);编码文本
std::string encoded = tree.encode(text);解码文本
std::string decoded = tree.decode(encoded);打印哈夫曼编码
tree.printCodes();