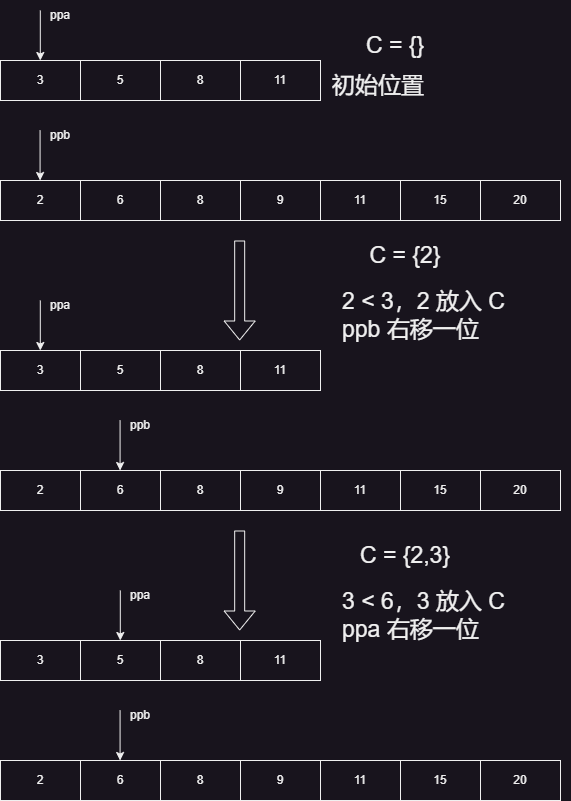
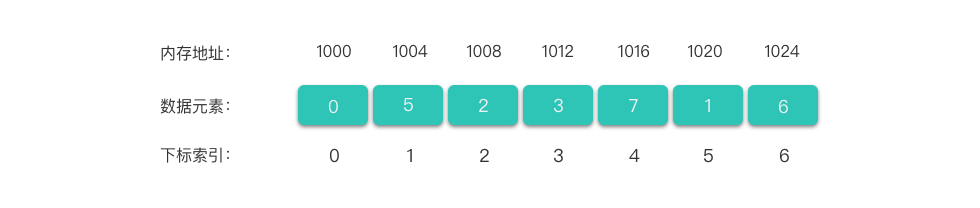
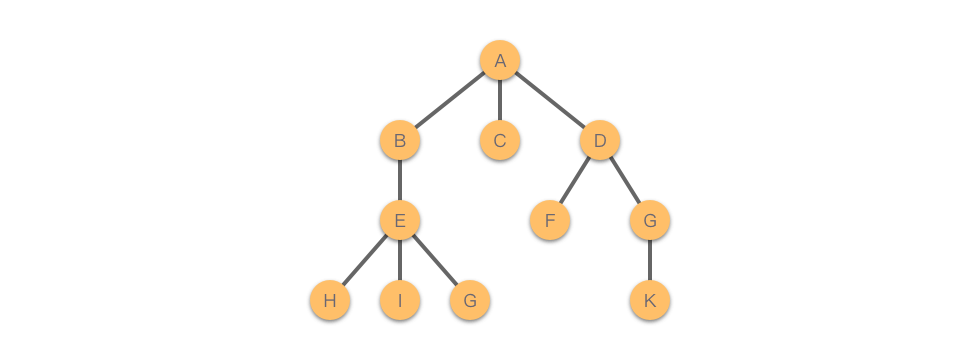
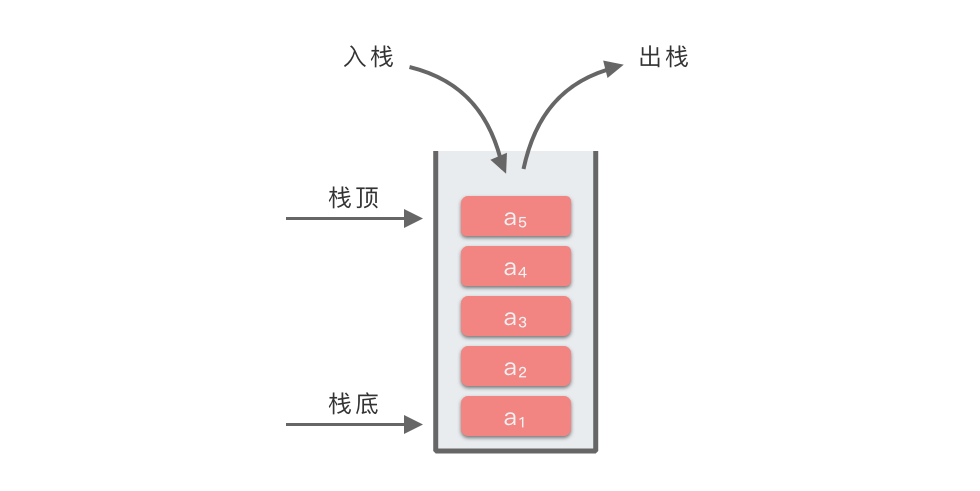
在卡上画上箭头,就成了链表
在上面的内容中,我们已经成功创建了一种线性的魔法卡册,它在四次元空间中是连续的。但是我们发现了两个问题:
- 这个空间量是提前申请的,但是不够灵活,如果卡片数量少,那其实没必要申请那么多空间。但如果申请的空间太小,卡片数量又恰巧比较多的话,那就没办法装下所有的卡了。
- 如果老板想要插入或者删除一张卡片,其时间复杂度都为 $O(N)$,如果 $n$ 太大,那么就需要占据你太多的时间。
为了改善这两个问题,让你可以减轻一点工作量(和四次元空间的压力),我们进一步修改卡册。
我们发现,顺序表有一个特点;它在四次元空间中是连续的。那能不能不连续呢?假设原本的卡片是“紧紧地左右黏在一起”的话,那么我们就把它们拆开,让卡片在四次元空间中离散地分布,由一根隐藏的线串联在一起。这样就可以不用提前申请一大块空间了。
那么这根线是什么呢?我们怎么利用这根线呢?现在你也进入了四次元空间,你找到了某一张卡片,然后你可以顺着这根线继续往后飘,你就可以找到下一张卡……以此类推。我们妥善地保存了这些数据。
那么我们也可以更抽象一点,这个线是一根虚拟的线。我们在卡片上画上一个箭头,使其指向下一张卡的方向,或者说坐标。那么实际上就形成了一条虚拟的线。
好了,现在你发明了链表。它是一种新的数据结构。准确来说,因为只有一个箭头,因此叫做单链表。

链表的关键在于学会其本质(即箭头),不要将链表当作一个孤立的数据结构去学习和记忆,要理解其本质的方法和思想。在之后的章节中,文章风格会减少对比喻的应用(相信之前已经能让读者建立起数据结构算法与实际问题之间的联系了)
不妨让我们回忆一下:
- 你的身份:无良公司的牛马员工,负责帮老板装一堆卡片
- 你的目的:设计出一种魔法卡册,完成老板的要求
- 老板的要求:访问、修改、查找、插入、删除
- 名词对应:
现实情况 专业解释 卡片 数据 卡册 数据结构 卡片的数量有多影响你的工作时长 时间复杂度
链表的结构定义和创建
结构定义
我们既然要往卡片上画箭头了,那么卡片上就不止它自身,还有箭头的信息,我们用一个结构体来封装一下:
// 一张卡片
struct LNode
{
ElemType Data; // 卡片的数据
LNode *next; // 指针,即卡片的箭头,它指向下一张卡片的地址
};
using LinkList = LNode *; // LinkList 为指向结构体 LNode 的指针类型不过还有一个问题,就是虽然每张卡片都有指向下一张卡片的箭头了,但是第一张卡片并没有上一张卡片指向它,为了统一和方便,我们会额外添加一个虚假的“0号节点”,也就是头节点,其指针指向首元节点,即真正的第一张卡片。
初始化
因此我们新建一个节点 L,使其指针置 nullptr 作为链表的初始化。
书本中的写法是较早版本的NULL,本文采用C++11标准后的nullter,其安全性更高。
// 初始化一个空的单链表 L
Status InitList(LinkList &L)
{
L = new LNode;
L->next = nullptr;
return OK;
}创建
下面演示将输入的 $n$ 个数据存入链表中。
// 建立一个链表 L,填入 n 个元素
Status CreateList(LinkList &L, int n)
{
InitList(L);
for (int i = 1; i <= n; i++)
{
LNode *p = new LNode; // 生成一个新的节点
cin >> p->Data;
p->next = L->next;
L->next = p;
}
return OK;
}因为我们定义*p是一个指针,所以【*p的Data】就不是p.Data了,而是p->Data。
单链表的操作
访问
抽象题意:访问链表 L 中的第 i 个节点,并返回其存储的数据
参数范围:i 的取值范围应当为 $1 \leq i \leq n$
错误可能:无
算法实现:我们从第一个节点,顺着链不断往后找,一直找到最后一个节点,或者中间就已找到了第 i 个位置。根据这点,我们思考实现:怎么顺着一个链不断往后找?我们建立一个指针,让它不断指向下一个节点即可;我们怎么判断已经找到了第 i 个位置?我们建立一个计数器 cnt,代表此时访问到第 cnt 个节点。如果有 cnt == i,那么就找到了第 i 个位置。
但是这里有一个问题:我们在分析参数范围时说,$1 \leq i \leq n$。在顺序表中我们会维护其长度 length,然而链表中我们并没有记录当前的数据量 ,这是为什么呢?让我们先来想一下 length 的优点:我们说,顺序表在空间中存储是连续的,也就是说只要知道首地址,我们可以方便地利用长度推断出一个位置的地址,在数组中表现为对下标的计算,因此维护 length 是有必要的。那么在链表中,它还是有必要的吗?链表在空间中的存储是离散的,知道了 length 除了方便我们判断参数是否合法之外,并没有什么好处,那我们就没有必要维护一个新的变量。
那么既然我们选择不维护 length 了,就需要想想在哪里判断位置 i 是否合法、如何判断位置 i 是否合法。刚才我们的一个关键操作是不断使得指针指向下一个节点,直到找到了第 i 个位置或找完最后一个节点。以这个操作为界,分成:
- 在此之前:此时指针刚指向第一个节点,
cnt == 1,没有可用的 - 在此之中:考虑两种不合法的情况:$i < 1$ 和 $i > n$。对于前者,有
cnt < 1,根本无法进入这个转移指针的循环,因此不能在循环中判断 - 在此之后:此时有
- 对指针,它要么指向了目标节点的下一个节点(找到了),要么指向空(到了最后一个节点后的节点,指向空)
- 对计数器,它要么刚好为
i(找到了),要么为链表长度 +1(到了最后一个节点还没找到)
那么,对于 $i < 1$,此时必然有 cnt >= 1 > i,可以判断;对于 $i > n$,此时一定有 cnt < i。
// 获取 L 中第 i 个元素的值,存储在 ans 中
Status GetElem(LinkList &L, int i, ElemType &ans)
{
LNode *p = L->next; // 现在指针 p 指向第一个节点
int cur = 0; // 代表现在移动到第 cur 个节点,初始 cur == 0,因为在头节点
while (p && cur < i) // 顺着链向后查找,直到 p 指向空或者遍历到第 i 个节点时代表查找结束
{
p = p->next; // p 会不断指向下一个节点
cur++; // 计数器增长
}
if (!p || cur > i) // 代表 i 不合法
return INFEASIBLE;
ans = p->Data;
return OK;
}时间复杂度:最坏情况下要全部找完,时间复杂度为 $O(N)$。
查找
抽象题意:访问链表 L 中值为 val 的节点,并返回其地址
参数范围:无
错误可能:无
算法实现:同理,我们顺着节点不断往后找即可
// 获取 L 中第一个值为 val 的节点的地址,并返回
LNode *FindElem(LinkList &L, ElemType val)
{
LNode *p = L->next;
while (p && p->Data != val)
p = p->next;
return p;
}时间复杂度:最坏情况下要全部找完,时间复杂度为 $O(N)$。
插入
抽象题意:将值为 val 的节点插入到链表中第 i 个节点的位置
参数范围:$1 \leq i \leq n+1$
错误可能:无
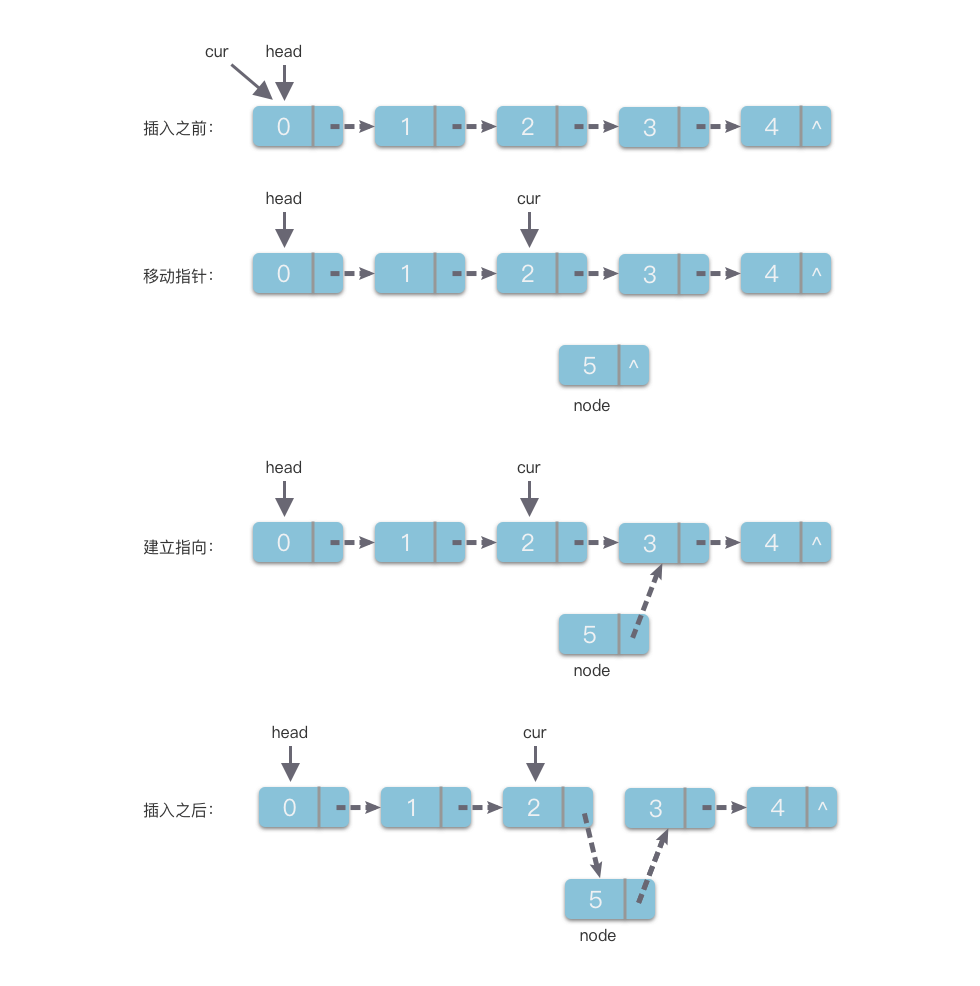
算法实现:想象往四次元空间里扔了一张卡片。对于这张卡片来说,它影响的对象有多少?显然,它只影响了它的前一张卡片,因为我们要将其箭头指向这张卡。然后,这张卡的箭头指向它的下一张卡片。按照这个思路我们只需要找到第 i-1 张卡片,修改其指针,指向需要插入的节点;再将需要插入的节点指针指向原本第 i-1 张卡片指向的节点。
// 在 L 中第 i 个节点处插入一个值为 val 的节点
Status ListInsert(LinkList &L, int i, ElemType val)
{
LNode *p = L->next;
int cur = 0;
while (p && (cur < (i - 1)))
{
p = p->next;
cur++;
}
if (!p || cur > (i - 1))
return INFEASIBLE;
// 此时查询到第 i-1 个节点,p 指向第 i 个节点
LNode *s = new LNode; // 预备插入的节点
s->Data = val;
s->next = p->next; // 预备插入的节点其地址应当为原第 i 个节点
p->next = s;
return OK;
}时间复杂度:最坏情况下要全部找完才能找到第 i-1 个节点,时间复杂度为 $O(N)$。
我们常说,链表在插入方面具有优势,是因为它没有数组整体右移的操作,而是只要修改指针。可是刚才通过分析,我们发现它们的时间复杂度都是 $O(N)$,这是怎么一回事呢?
首先需要明确的是,在现实生产环境中,受到各种物理等因素的影响,链表未必优于数组,接下来我们只讨论在理论情况下的说法。
可以认为,数组的插入操作,由一个 $O(1)$ 的查询操作和一个 $O(N)$ 的修改操作组成;链表的插入操作,由一个 $O(N)$ 的查询操作和一个 $O(1)$ 的修改操作构成。但其中,数组的修改操作分为两个部分:读(读入位置)和写(写入值)构成;链表的查询操作只有读的部分。因此链表的综合时间复杂度是更优的。
也有一种说法是,现实中很少有需求是“在第 $i$ 个节点的位置插入新的节点”,而是删掉某一些特定的节点,在此时不需要查询操作,$O(1)$ 复杂度的修改操作复杂度是很低的。
删除
抽象题意:删除第 $i$ 个节点
参数范围:$1 \leq i \leq n$
错误可能:无
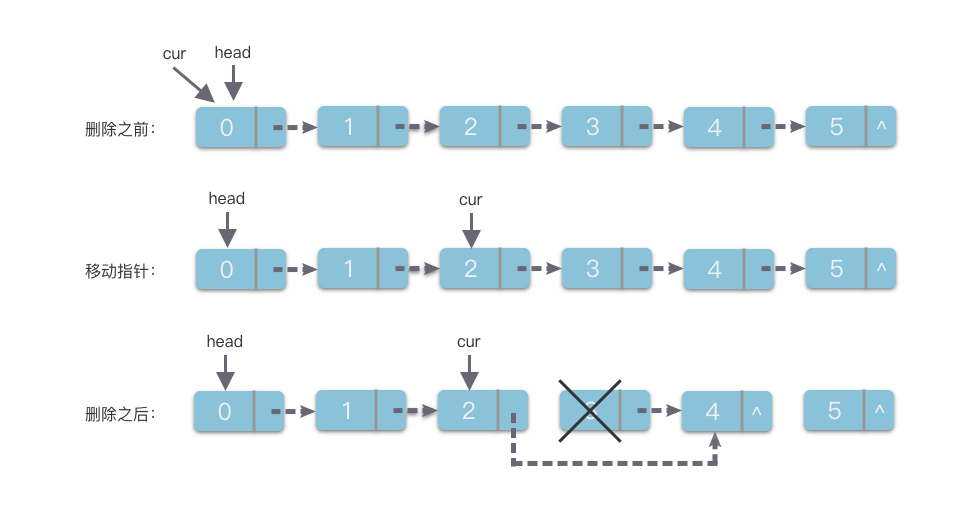
算法实现:类似于单链表的插入。我们的目的是将原本第 $i-1$ 个节点的指针“连接到”第 $i+1$ 个节点上,然后再删掉第 $i$ 个节点。
// 删除 L 的第 i 个节点
// 实际上是把第 i-1 个节点的指针指向第 i+1 个节点
Status ListDelete(LinkList &L, int i)
{
LNode *p = L->next;
int cnt = 0;
while (p && (cnt < (i - 1)))
{
p = p->next;
cnt++;
}
// 此时查询到第 i-1 个节点,p 指向第 i 个节点
if (!p || cnt > (i - 1))
return INFEASIBLE;
LNode *s = p->next; // 暂时存储 p->next,即第 i 个节点,预备删除
p->next = s->next;
delete s;
return OK;
}我们需要更多的箭头!
在刚才被称为链表的魔法卡册中,我想有一个疑问是显然可见的……为什么我们只给每张卡片画了一个箭头,指向它的下一个节点?可以有更多的箭头吗?多的箭头可以指向它的上一个节点吗?这个箭头可以指向另一个节点吗?……
是的,这就是学习链表的意义:掌握箭头(即指针)的使用。如果这个箭头指向它的上一个节点,那么我们就创造了双向链表。如果这个箭头指向另一个节点,那么很有可能会变化成链式存储的图……
我们先介绍两种比较简单的,分别是循环链表和双向链表。
循环链表
循环列表非常简单,它仅仅添加了一个箭头:将最后一张卡片指向第一张卡片。这样就构成了一个循环,就像是手拉手的小朋友围成了一个圈一样。代码实现也非常简单,只要将最后一个节点的指针指向的地址修改为第一个节点的地址(即 $L$),也就是说判断是否遍历到最后一个节点的条件变为:
p != L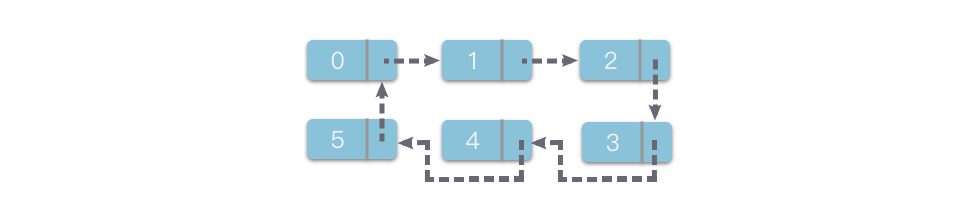
双向链表
双向链表则是添加了一个箭头,每个卡片有一个箭头指向后一张卡片,有一个箭头指向前一张卡片。更计算机的表述是:每个节点有一个指针指向其后继,有一个指针指向其前驱。
// 双向链表存储结构
struct DulNode
{
ElemType data; // 数据域
DulNode *prior; // 指向前驱
DulNode *next; // 指向后继
};
using DulLinkList = DulNode *;如果你理解单链表的操作,那么双链表的操作就水到渠成了。但是要注意双链表的每个节点有两个指针,操作的时候要注意节点的两个指针都有可能变化。
链表总结
- 链表是实现线性表的链式存储结构的基础,它使用一组任意的存储单元(可以是连续的,也可以是不连续的),来存储一组具有相同类型的数据。
- 链表最大的优点在于可以灵活地添加和删除元素。
- 链表进行访问、改变元素操作的时间复杂度为 $O(N)$
- 链表进行头部插入、头部删除元素操作的时间复杂度为 $O(1)$
- 链表进行尾部插入、尾部删除元素操作的时间复杂度为 $O(N)$
- 链表在普通情况下进行插入、删除元素操作的时间复杂度为 $O(N)$
链表解决约瑟夫问题
数据结构永远是来解决实际问题的!
下面我们来看一个具体的小游戏:
问题:$n$ 个人围成一圈,从第一个人开始报数,数到 $m$ 的人出列,再由下一个人重新从 $1$ 开始报数,数到 $m$ 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
输入:输入两个整数 $n$,$m$
输出:输出一行 n 个整数,按顺序输出每个出圈人的编号。
你可能会想赶紧回到前面开始找哪个操作能实现这个过程……先别急着拼凑我们给出的模板,分析这个过程。
$n$ 个人围成一圈:需要输入 $n$ 个数据并以此存储在链表中,因为围成一圈所以应该是循环链表
数到 m 的人出列:出列就是删除,查找第 $m$ 个节点并将其删除。此时就需要改变指针,将原 $m-1$ 号节点指针指向原 $m+1$ 号节点,再删除第 $m$ 个节点。
直到所有的人都出圈:结束的条件是不再有任何一个节点存在。
只要你会用指针,甚至都不用看上面的内容,你就可以完成这道题。
#include <iostream>
using namespace std;
typedef struct LNode
{
int data;
struct LNode *next;
} LNode;
// 建立循环链表,共 n 个节点,返回首元节点
LNode *CreateList(int n)
{
LNode *head = new LNode;
head->data = 1; // 第一个节点的序号为 1
LNode *now = head; // 代表当前的节点
for (int i = 2; i <= n; i++)
{
LNode *p = new LNode; // 新建一个节点
p->data = i; // 每一个节点的数据,即序号,第 i 个节点的序号是 i
now->next = p; // 当前节点指向新节点
now = p; // 修改 now 到新节点
}
now->next = head; // 形成循环
return head;
}
// 解决约瑟夫问题的代码,有 n 个小朋友,数到 m 时出列
void solve(int n, int m)
{
LNode *head = CreateList(n); // 首元节点
LNode *now = head; // 当前节点
LNode *prev = nullptr; // 上一个节点
while (n > 0) // 循环终止条件是找到最后一个人
{
for (int i = 1; i < m; i++)
{
prev = now;
now = now->next;
}
cout << now->data << " "; // 输出当前节点的序号
prev->next = now->next; // 修改 i-1 的指针到 i+1
delete now; // 删除当前节点
now = prev->next; // 当前节点是删除节点的下一个
n--; // 人数 -1
}
cout << "\n"; // 最后一个换行
}
int main()
{
int n, m; // 题目要求的输入
cin >> n >> m;
CreateList(n);
solve(n, m);
return 0;
}为什么我各种链表操作和之前给出的写法不一样?
这种写法是针对当前问题的特化性写法,删掉了一些无用操作,使得整体更加简洁。而原本的写法更加具有一般性。数据结构最终应用于实际的需求而不是记忆。不要再背代码了!!!
然而我也不知道考试的要求,请结合你们老师的说法和实际的考试内容自行判断我的言论的合理性。