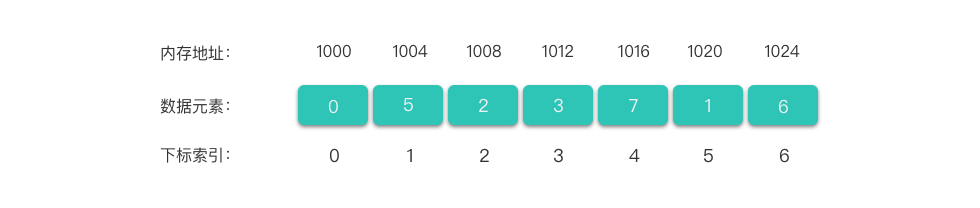
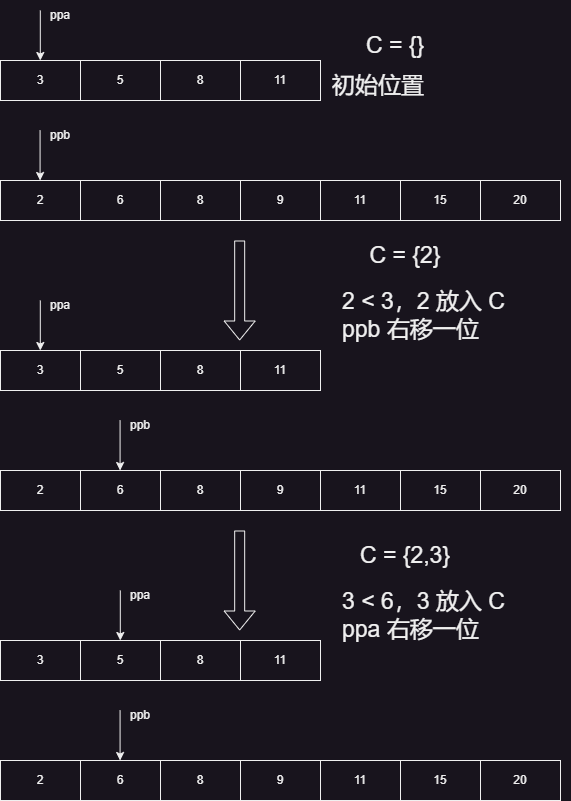
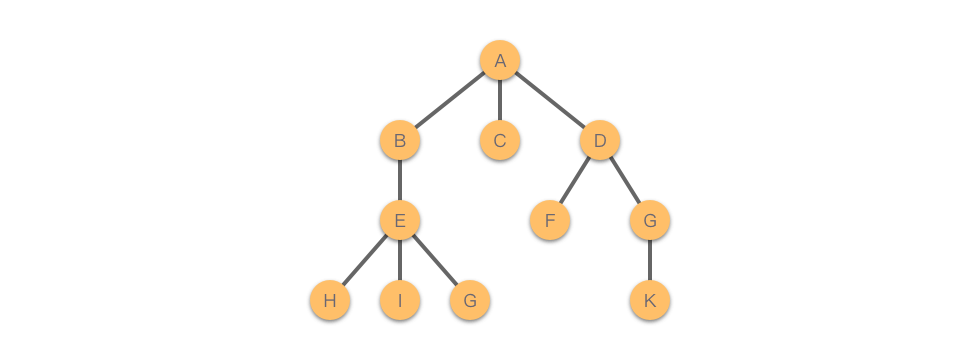
我们现在只关注头和尾
下班之后,你决定吃一罐薯片。
正如牛顿被苹果砸到之后思考,为什么苹果是往下落不是往上飞一样;你开始思考:通常来说我们每次都只能拿最上面一块薯片,那中间的薯片我们根本不关心。一个薯片罐如果就是一个数据结构的话,那么我们只处理尾端的元素,不关心中间的元素。这样的数据结构有没有价值呢?
想象你记忆了一串数字,例如 3 65 23 5 34 1 30 0,现在我要求你把它们倒着背出来。那么这个过程,就相当于从后往前一个一个拿出元素,正如薯片一个一个拿出来吃掉直到薯片罐变得空空如也。
这就是栈。
先进后出的栈
正如标题所言,栈是一种先进后出(Last in First Out,LIFO)的线性表,是一种只允许在表的一端进行插入和删除操作的线性表。
不过既然它已经是一个独立的数据结构了,我们就给它一些方便的名字负责交流。栈中允许交流插入和删除的一段称为栈顶(top);另一端则称为栈底(bottom)。当表中没有任何数据元素时,称之为空栈。因此:
- 栈的插入操作又称为入栈或进栈
- 栈的删除操作又称为出栈或退栈
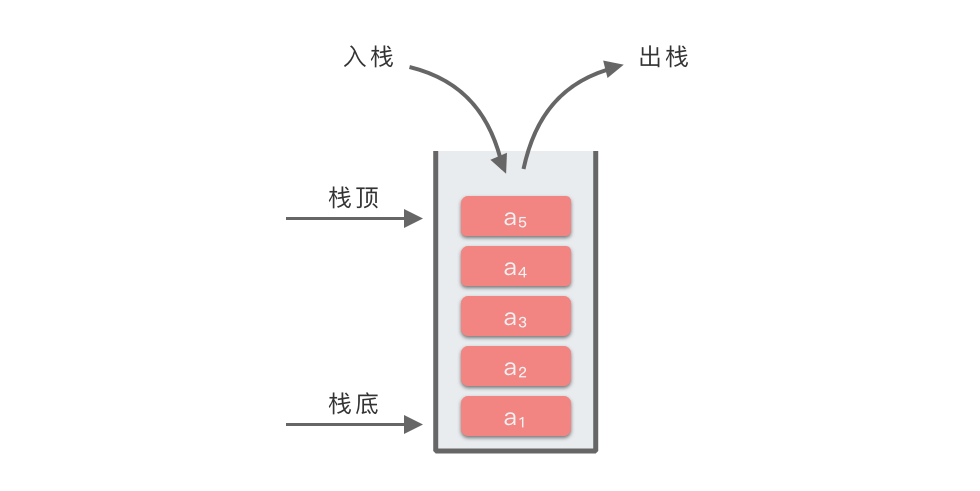
结合前面对顺序表和链表的操作,以及我们拿薯片的过程,让我们思考栈的操作:
| 薯片 | 栈的操作 |
|---|---|
| 往薯片罐里放薯片 | 将元素放入栈,“入栈” |
| 从薯片罐内拿薯片 | 将元素拿出栈,“出栈” |
| 往薯片罐里看一眼薯片的口味 | 查看栈顶的元素 |
| 往薯片罐里看一眼薯片吃完了没 | 检查栈是否为空栈 |
那么这个过程,我们发现,我们总是只关注薯片罐内最顶部的薯片。如果记录其位置,那么只有该薯片的位置在上下浮动。既然薯片罐是连续的,我们能不能将顺序表改造成一个栈呢?当然能!
我们把薯片罐放倒,就变成了我们熟悉的横向的顺序表。用一个指针 top 记录最右边的元素的位置,放入元素,其位置右移一位;取出元素,其位置左移一位;查看元素,就返回数组中该位置存储的元素……

在我们自己动手搓一个栈之前,先让我们看看那些大佬们写的栈,即 STL stack,它是被内置于 C++ 语言中的库,可以直接调用其函数来实现栈。下面仅展示其常用的几个函数:
#include <iostream>
using namespace std;
stack<ElemType> st; // 新建一个名为 st 的空栈
st.empty(); // 返回栈是否为空,若为 1,则栈为空
st.pop(); // 弹出栈顶的元素
st.push(val); // 将值为 val 的元素入栈
st.size(); // 返回栈的长度(即栈内的数据元素)
st.top(); // 返回栈顶的元素实现 STL 栈
不要觉得我们调用的库和函数很高级,作为顶级 C 语言魔法使用者,其实我们完全可以模拟出来!尽管在效率上可能不如 STL stack,但是在功能上几乎是完全一致的。
我们前面已经学过了顺序表和链表,其本质即为数组和指针。我们可以用两种方式实现栈(和之后几乎所有的数据结构)。对于前者而言,关键在于将其想象成连续的结构,就像是连续排列的卡片,使用数组和你可能需要的索引;对于后者而言,关键在于将将其想象成多张分散的卡片,但用箭头指向其他卡片,使用节点和指针。
顺序栈的写法
根据上面的描述和演示,我们可以先用顺序表实现一个栈:
// 栈的存储结构
#define MAXSIZE 100 // 栈的最大长度
typedef struct
{
ElemType *top; // 栈顶的指针
ElemType *base; // 栈底的指针
int StackSize; // 栈可用的最大容量
} SqStack;
// 构造一个空栈 S
Status InitStack(SqStack &S)
{
S.base = new ElemType[MAXSIZE]; // 为栈分配一个最大容量为 MAXSIZE 的数组空间
if (!S.base) // 存储分配失败
return OVERFLOW; // 栈溢出
S.top = S.base; // 现在栈是空的,栈顶指针和栈底指针是重合的
S.StackSize = MAXSIZE; // 栈可用的最大容量就是 MAXSIZE
return OK; // 创建成功
}
// 判断栈是否为空,为空则返回 ERROR(1),否则返回 OK(0)
Status Empty(SqStack &S)
{
if (S.top == S.base)
return ERROR;
return OK;
}
// 将栈尾出栈
Status Pop(SqStack &S)
{
if (S.top == S.base) // 此时栈为空
return ERROR;
S.top--;
return OK;
}
// 将值为 val 的元素入栈
Status Push(SqStack &S, ElemType val)
{
if (S.top - S.base == S.StackSize) // 当前已经栈满
return ERROR;
*S.top = val; // 当前栈顶的位置放入 val 元素
S.top++; // 栈顶的指针右移
return OK;
}
// 返回栈的大小
int Size(SqStack &S)
{
return S.top - S.base;
}
// 返回栈顶的元素,将值存储在 res 中
Status Top(SqStack &S, ElemType &res)
{
if (S.top - S.base == 0)
return ERROR;
res = *(S.top - 1);
return OK;
}链式栈
下面的代码演示了链式栈的写法。
// 栈的存储结构
#define MAXSIZE 100 // 栈的最大长度
typedef struct StackNode
{
ElemType data; // 该节点存储的数据
struct StackNode *next;
} StackNode;
// 创建一个链表
typedef struct LinkStack
{
StackNode *top; // 栈顶指针
int size; // 用于记录栈内的元素个数
} LinkStack;
// 构造一个空栈 S
Status InitStack(LinkStack &S)
{
S.top = nullptr;
S.size = 0;
return OK;
}
// 判断栈是否为空,为空则返回 1,否则返回 0
Status Empty(LinkStack &S)
{
return S.top == nullptr;
}
// 将栈尾出栈
Status Pop(LinkStack &S)
{
if (S.top == nullptr) // 此时栈为空
return ERROR;
StackNode *tmp = S.top; // 新建一个临时节点,用该节点临时保存栈顶
S.top = S.top->next; // 修改栈顶指针
delete tmp; // 删除该节点
S.size--; // 减少计数器
return OK;
}
// 将值为 val 的元素入栈
Status Push(LinkStack &S, ElemType val)
{
StackNode *p = new StackNode; // 新建一个节点
p->data = val; // 该节点存储数据
p->next = S.top; // 将新节点插入栈顶
S.top = p; // 更新栈顶指针
S.size++; // 计数器增加
return OK;
}
// 返回栈的大小
int Size(LinkStack &S)
{
return S.size;
}
// 返回栈顶的元素,将值存储在 res 中
Status Top(LinkStack &S, ElemType &res)
{
if (S.size == 0)
return ERROR;
res = S.top->data;
return OK;
}优雅地打包代码
上面的代码展示了栈的底层原理。但是从函数的调用方式上来看,似乎还有一些差别……以顺序栈为例,如果要创建一个名字为 st 类型为 int 的栈,其写法分别为:
stack<int> st; // STL 的写法
SqStack st;
Init(st); // 我们手搓的写法这样看还是有一些遗憾,能不能做得更完美一些?让我们回忆一下大一下学期,有关 C++ 面向对象的知识。我们曾经用类将同一类的数据、定义、实现等封装在一起,就像是打包在一个箱子里一样。如果我们可以将栈写成一个类,那么我们就可以完美实现 STL stack 栈,至少看上去差不多!
#include <iostream>
#include <stdexcept> // 用于抛出异常
using namespace std;
template <typename T> // template 用来声明一个模板,typename 是类型参数,可用任何数据类型,例如 int/char/double 等代替
class myStack
{
private:
T *data; // 指向动态分配的数组
size_t maxSize; // 栈的最大容量
int topIndex; // 栈顶索引
public:
// 构造函数,初始化栈
myStack(size_t maxSize) : maxSize(maxSize), topIndex(-1)
{
data = new T[maxSize]; // 动态分配内存
if (!data)
throw bad_alloc(); // 分配失败抛出异常
}
// 析构函数,释放内存
~myStack()
{
delete[] data;
}
// 检查栈是否为空
bool empty() const
{
return topIndex == -1;
}
// 返回栈中元素的数量
size_t size() const
{
return topIndex + 1;
}
// 返回栈顶元素,分成可修改的和不可修改的
T &top()
{
if (empty())
throw out_of_range("空栈"); // 空栈
return data[topIndex];
}
const T &top() const
{
if (empty())
throw out_of_range("空栈");
return data[topIndex];
}
// 向栈中加入元素
void push(const T &value)
{
if (size() == maxSize)
throw overflow_error("栈满"); // 栈满
data[++topIndex] = value;
}
// 移除栈顶元素
void pop()
{
if (empty())
throw out_of_range("空栈");
--topIndex;
}
// 删除栈内所有的元素
void clear()
{
while (!empty())
pop();
}
};
栈的应用
所有需要先进后出的问题都可以用栈来解决。——或者说,所有可以用薯片罐来分析的问题都可以用栈来解决。
现在让我们来看一道题:
问题:给出一个只有小写英文字母、运算符(
+、-、*、/)和左右小圆括号构成,以@作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则输出YES;否则输出NO。表达式长度小于 255,左圆括号少于 20 个。输入:仅一行,表达式。
输出:仅一行,
YES或NO。输入输出样例:
- #1
2*(x+y)/(1-x)@
- 输入
YES
- 输出
- #2
(25+x)*(a*(a+b+b)@
- 输入
NO
- 输出
根据小学二年级就学过的括号匹配知识,我们知道:一个右括号必定对应一个左括号。而且一个左括号,必定是和右侧距离其最近的右括号匹配。想象有两种颜色的薯片:红色的和黄色的。你是个挑剔的人,你只能吃一块红色的、再吃一块黄色的。往薯片罐里不断投入薯片,如果是红色的:就放进去,你要等下下一块黄色的出现;如果是黄色的,你要检查当前最上面的薯片是不是红色的,若是,你就把两块都抓出来吃掉;如果不是,那么这桶薯片就是糟糕的薯片:因为它永远等不来它的上一块红色薯片了,真是悲剧。
下面让我们来写代码。
STL Stack,除了调用方式和速度可能有差别之外,都可以实现一个栈的功能。读者可以尝试用刚才自己写出来的栈来解决。#include <iostream>
#include <stack>
using namespace std;
string s; // 用于输入表达式
stack<char> st; // 一个 char 类型的栈,命名为 st
int main()
{
cin >> s; // 输入表达式
int i = 0; // 代表当前查询到表达式的第 i 位
while (s[i] != '@') // 表达式是到 @ 结束的
{
if (s[i] == '(') // 我们只关心左右括号,如果是左括号,入栈
st.push(s[i]);
else if (s[i] == ')')
{
if (!st.empty() && st.top() == '(')
// 如果栈不为空且当前栈顶为左括号,括号匹配,删除栈顶的左括号。
// 如果不加上对栈是否为空的判断,会导致空栈时无法读取栈顶元素而报错
st.pop();
else
{
cout << "NO"; // 括号不匹配,则输出 NO
return 0;
}
}
i++; // 指示器不断向右移动
}
if (!st.empty()) // 栈内还有元素,说明括号未匹配完成
cout << "NO";
else
cout << "YES";
return 0;
}先进先出的队列
刚才我们在研究栈的时候吃了太多的薯片,于是你决定去超市买薯片。
超市的人太多了!你必须要排队!队首的人结完账之后就会离开,队尾的人又在源源不断地涌入,队伍中间的人一般会觉得自己都排了那么久了干脆再等等吧,一般都不会动。——这和薯片桶的情况是类似的,只是这一次我们把薯片桶的底部也打开了,现在更像是一个管道,我们从一端拿薯片,从一端塞薯片,这样原先底部的薯片最终会被你吃掉。
既然距离结账还有一点时间,我们就来研究一下你的处境吧:一个队列(queue)!
队列也是一种线性表数据结构,它只允许你在表的一端进行插入操作,另一端进行删除操作。其中,允许插入的一端叫做队尾(rear),允许删除的一端叫做队首(front)。队列的插入操作又叫做入队,删除操作则叫做出队。
和栈不同,队列是一种先进先出(First in First out) 的线性表,简称为FIFO结构。
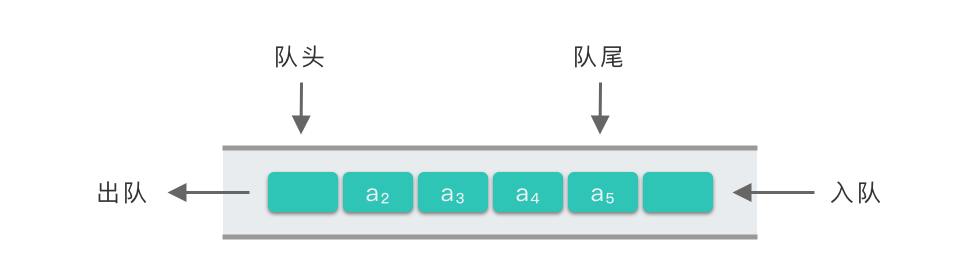
其动态演示参照:

但是,队列和栈的实现是基本一致的。唯一的区别是现在你要维护两个指针了,它们一个在队首,一个在队尾。如果有元素入队,那么队尾就要向后移动;如果有元素出队,那么队首就要向后移动。

不过有一个问题,这个空间可不是无限的。队首和队尾都在向后移动(比较像一条蠕动的毛毛虫),那些没有装数据的空间岂不是就被浪费了吗?聪明的前人们已经想过了:线性的空间终有尽头,但如果把它绕成一个圈,岂不是可以重复回去利用那些没有用到的空间了吗?
假设最大长度是 maxSize,那么如果队列的第 maxSize-1 位置被占用之后,只要队列前面还有可用空间,新的元素加入队列时就可从第 0 个位置开始继续插入。假设队尾的索引是 rearIndex,那么其前进一个位置时就是:
rearIndex = (rearIndex + 1) % maxSize;我们还是试图还原 STL queue 中的所有常用函数。
顺式存储队列
#include <iostream> #include <stdexcept> using namespace std; // 模板类 ArrayQueue,支持任何数据类型 template <typename T> class ArrayQueue { private: T *data; // 动态数组,存储队内元素 size_t maxSize; // 最大容量 size_t frontIndex; // 队首索引 size_t rearIndex; // 队尾索引,指向下一次插入的位置 size_t count; // 元素数量 public: // 构造函数,初始化队列大小为给定的容量 explicit ArrayQueue(size_t maxSize) : maxSize(maxSize), frontIndex(0), rearIndex(0), count(0) { data = new T[maxSize]; // 为队列分配内存 } // 析构函数,释放队列内存 ~ArrayQueue() { delete[] data; } // 向队尾添加元素 void push(const T &value) { if (count == maxSize) // 队列已满 throw overflow_error("队列已满"); // 抛出异常 data[rearIndex] = value; // 存储新元素 rearIndex = (rearIndex + 1) % maxSize; // 移动队尾指针,循环队列 ++count; // 元素加一 } // 移除队首元素 void pop(const T &value) { if (empty()) // 队列空 throw underflow_error("队列为空"); // 抛出异常 frontIndex = (frontIndex + 1) % maxSize; // 移动队首指针 --count; // 元素减一 } // 检查队列是否为空 bool empty() const { return count == 0; } // 返回队列中元素的数量 size_t size() const { return count; } // 返回队首元素 T &front() { if (empty()) throw underflow_error("队列为空"); return data[frontIndex]; } const T &front() const { if (empty()) throw underflow_error("队列为空"); return data[frontIndex]; } // 返回队尾元素 T &back() { if (empty()) throw underflow_error("队列为空"); return data[rearIndex]; } const T &back() const { if (empty()) throw underflow_error("队列为空"); return data[rearIndex]; } };链式存储队列
#include <iostream> #include <stdexcept> using namespace std; template <typename T> class LinkQueue { private: // 链表节点结构 struct Node { T data; Node *next; Node(const T &value) : data(value), next(nullptr) {} // 节点构造函数 }; Node *frontNode; // 指向队首节点 Node *rearNode; // 指向队尾节点 size_t count; // 记录队列中节点的数量 public: // 构造函数,初始化空队列 LinkQueue() : frontNode(nullptr), rearNode(nullptr), count(0) {} // 析构函数,销毁链表,释放内存 ~LinkQueue() { while (!empty()) pop(); } // 向队尾添加元素 void push(const T &value) { Node *newNode = new Node(value); // 创建一个新的节点 if (rearNode) rearNode->next = newNode; // 连接到新的节点上 else frontNode = newNode; // 若为空队列,将其直接作为首节点 rearNode = newNode; // 更新队尾指针 ++count; } // 移除队首元素 void pop() { if (empty()) // 检查队列是否为空 throw underflow_error("队列为空"); Node *tmp = frontNode; frontNode = frontNode->next; // 移动到下一个节点 if (!frontNode) rearNode = nullptr; // 若队列为空,则更新尾指针 delete tmp; // 释放移除节点的内存 --count; } // 检查队列是否为空 bool empty() const { return count == 0; } // 返回队列中元素的数量 size_t size() const { return count; } // 返回队首元素 T &front() { if (empty()) throw underflow_error("队列为空"); return frontNode->data; } const T &front() const { if (empty()) throw underflow_error("队列为空"); return frontNode->data; } // 返回队尾元素 T &back() { if (empty()) throw underflow_error("队列为空"); return rearNode->data; } const T &back() const { if (empty()) throw underflow_error("队列为空"); return rearNode->data; } };总结
真是完美的一天!吃到了薯片,还排了队(?)更重要的是我们从中学到了两种有趣的数据结构,分别是先进后出的栈,因为先放进去的薯片得等到后面才能拿到;还有先进先出的栈,因为先到收银台的人会先结账离开。
到此为止,我们已经学习了顺序表和链表,它们分别对应两种基础:数组,它是连续的一段;指针,它作为一根隐形的线将各个节点连接在一起。但无论是数组还是指针,它们都可以看作一条线,因为对于每一个元素(除了第一个和最后一个)之外,都只有前面和后面两个元素与之相邻。
通过实际上的线(物理相邻的数组)和虚拟的线(通过指针相连的链表),我们可以进一步实现其他的数据结构。为了解决生活中有些时候,我们只关心首尾而不关心中间部分的问题,例如吃最上面的薯片,再例如排队,我们研究出了栈和队列两种数据结构。
说了这么多,主要是希望大家建立起一个认知过程,即“数据结构永远是为了解决实际问题存在的”,和“任何数据结构其实都是从之前的数据结构改造而来的”。我们因为要收集、整理一堆数据,使用了顺序表;因为顺序表一定要是连续的,不够灵活,我们利用箭头(即指针)研究出了链表;在它们的基础上,我们特化地为了解决只关心头尾处理的问题,砍掉了冗余的部分,只保留了对头尾操作的极致操作,从而产生了栈和队列。
像这样,我们要深入数据结构中更复杂的地方了。这简直是从自行车到摩托车的飞跃。
修改日志
修正了部分标题未居中的错误。