Kruskal 算法

原理

Kruskal 算法由两个步骤构成：

• 对边的长度贪心并加入 $T$ 中。先对边长排序，然后依次把最短的边加入到 $T$ 中。

• 判断圈。每次加入边，判断它是否和已经加入 $T$ 的边形成了圈，也就是判断连通性。可以使用 DFS 或者 BFS，但是最高效的方法是 并查集。

模板代码

下面的代码作为最小生成树的模板题，解决了P3366 【模板】最小生成树问题。

#include <iostream>
#include <algorithm>

using namespace std;

int read()
{
    int x = 0, f = 1;
    char ch = 0;
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

const int maxN = 5005;
const int maxM = 2e5 + 5;

struct Edge
{
    int u, v, w;
} edge[maxM];

int s[maxN]; // 并查集

bool cmp(Edge a, Edge b)
{
    return a.w < b.w;
}

// 并查集 - 查询
int find_set(int x)
{
    if (x != s[x])
        s[x] = find_set(s[x]);
    return s[x];
}

int N, M;

void kruskal()
{
    sort(edge + 1, edge + M + 1, cmp);
    for (int i = 1; i <= N; i++)
        s[i] = i;
    int ans = 0, cnt = 0; // cnt 存储已经放入 T 中的边数
    for (int i = 1; i <= M; i++)
    {
        if (cnt == N - 1)
            break;
        int e1 = find_set(edge[i].u);
        int e2 = find_set(edge[i].v);
        if (e1 == e2)
            continue;
        else
        {
            ans += edge[i].w;
            s[e2] = e1;
            cnt++;
        }
    }
    if (cnt == N - 1)
        printf("%d\n", ans);
    else
        printf("orz");
}

int main()
{
    N = read();
    M = read();
    for (int i = 1; i <= M; i++)
    {
        edge[i].u = read();
        edge[i].v = read();
        edge[i].w = read();
    }
    kruskal();
    return 0;
}

Prim 算法

执行过程

设最小生成树中的点的集合为 $U$，开始时最小生成树为空，所以 $U$ 为空。以下图为例，执行步骤如下：

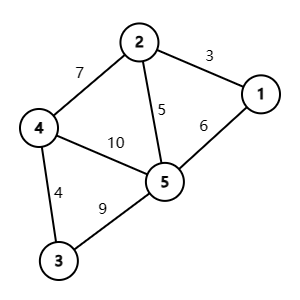
1. 任取一点，如点 $1$，放到 $U$ 中，$U = {1}$。
2. 找离集合中的点最近的邻居，即点 $1$ 的邻居，为点$2$，放到 $U$ 中，$U = {1,2}$。
3. 找离 $2$ 最近的点，为 $5$，放入 $U$ 中，$U = {1,2,5}$
4. 离 $5$ 最近的此时是 $1$（上一步已经构造了 $2 -5$，所以不考虑那一条边），但 $1$ 已经在集合中了，我们就选择 $4$。
5. 以此类推，直到所有点都在 $U$ 中。

观察发现，Prim 算法的思想和 Dijkstra 算法基本相同。但是 Dijkstra 算法需要更新 $U$ 中所有点到起点的距离，Prim 算法不需要。同理地，用优先队列优化 Prim 算法能最终将复杂度降低至 $O(m\log_2n)$。

模板代码

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int read()
{
    int x = 0, f = 1;
    char ch = 0;
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

const int maxN = 5005;
const int maxM = 2e5 + 5;

struct edge
{
    int to, w;
    edge(int a, int b) { to = a, w = b; }
};

struct node
{
    int id, dis;
    node(int a, int b) { id = a, dis = b; }
    bool operator<(const node &u) const { return dis > u.dis; }
};

int n, m;

bool done[maxN];
vector<edge> G[maxM];

void prim(int n)
{
    int s = 1;
    for (int i = 1; i <= n; i++)
        done[i] = false;
    priority_queue<node> q;
    q.push({node(s, 0)}); // 从 s 点开始处理数据
    int ans = 0, cnt = 0;
    while (!q.empty())
    {
        node u = q.top();
        q.pop();
        if (done[u.id])
            continue;
        done[u.id] = true;
        ans += u.dis;
        cnt++;
        for (int i = 0; i < G[u.id].size(); i++)
        {
            edge y = G[u.id][i];
            if (done[y.to])
                continue;
            q.push({y.to, y.w});
        }
    }
    if (cnt == n)
        printf("%d\n", ans);
    else
        printf("orz");
}

int main()
{
    n = read();
    m = read();
    for (int i = 1; i <= m; i++)
    {
        int a, b, w;
        a = read();
        b = read();
        w = read();
        G[a].push_back(edge(b, w));
        G[b].push_back(edge(a, w));
    }
    prim(n);
    return 0;
}